## 总结 Diffusion 的操作其实非常简单,核心算法的框架伪代码如下图所示:  其中 `Training` 的部分,主要包含了 **Add Noise** 这个步骤(Forward Process)。每次我们选取一张图 $x_0$ (真值),一个 $[1, T]$ 的数 $t$,和一个高斯噪声 $\epsilon \sim \mathcal{N}(0, I)$ 。每次把高斯噪声 $\epsilon$ 加给 $x_0$ 的步骤就是 add noise。**一个比较精巧(奇妙)的操作时这个 $t$**。当然,如果从 Autoregressive 的角度来看待 Diffusion,这个 $t$ 是非常合理的。 在 `Sampling` 部分,主要是包含了一个 **Denoise** 的步骤 (Reverse Process)。其中,一个用以预测整体噪声的网络 $\epsilon_{\theta}$ 是我们优化的目标。$\epsilon_{\theta}$ 要生成在 `Training` 阶段对应位置加过噪声的图片中,**真实的噪声分布**。我们**不可以把 Denoise** 简单的看成是一个 add noise 的逆过程。原因有两点: 1. Denoise 过程中消去的噪声是 $\epsilon_{\theta}$ 的预测值而非真实值。 2. 注意到 `Sampling` 阶段的末尾加上了一个神秘 $\sigma_t\mathbf{z}$。这个东西非常有说法。在这里我想提供李宏毅老师课中的一个解释。以 GPT 为例,如果预测的下一个位置永远是 Confidence 最高的 candidate,那么生成出来的文本很有可能是一段不断重复一个意思的段落。因此,LLM 中也会类似地加上一个这样的随机噪声。同理可得,如果没有在 denoise 阶段加上这个随机噪声,那么我们生成的图像可能是一张单一颜色的图像。 因此对于 denoise 过程,我目前的理解是:由于真实的图像的噪声可必然是一个**比我们目前假设的噪声分布——即高斯分布,更加复杂的分布。** 因此,Diffusion 的 denoise 实际上是在产生一个其噪声符合一个低级(简单)分布的图像。 ## Add Noise 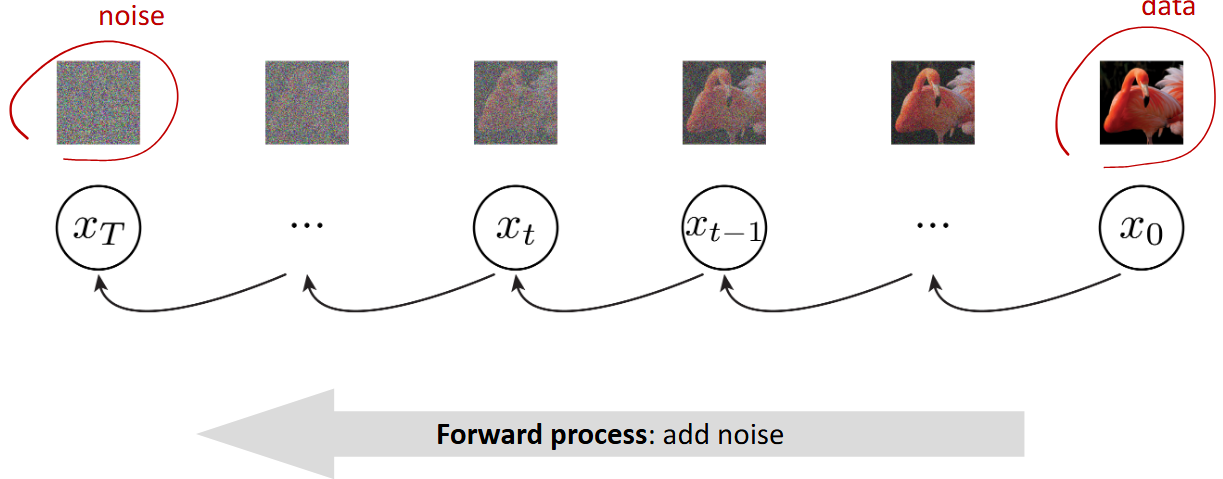 ### Definition 在 DDPM(Denoising Diffusion Probabilistic Models)中,前向过程定义为一个 **马尔科夫链**: $$ q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t\mathbf{I}) $$ 其中: - $\beta_t$ 是一个噪声方差的超参数(通常很小,且逐渐变小) - 条件分布是高斯分布,均值缩小原输入,方差是 $\beta_t$ 也就是说,每次我们加上去一个高斯噪声 $\epsilon \sim \mathcal{N}(0, \mathbf{I})$ 给 $x_{t}$: $$ x_t = \sqrt{1 - \beta_t} x_{t - 1} + \beta_t\epsilon $$ 从这个式子我们可以看出: - **均值**:$\sqrt{1 - \beta_t} x_{t - 1}$,表示对输入的逐步衰减。 - **方差**: $\beta_t$ ,表示每一步加的高斯噪声强度。 这样设计的好处是:**整个过程可以解析化地推出任意 $t$ 时刻的分布:** $$ q(x_t|x_0) = \mathcal{N}(\sqrt{\bar{\alpha_t}}x_0, (1 - \bar{\alpha_t})\mathbf{I}) $$ 其中:$\bar{\alpha_t} = \prod_{i = 1}^{t} (1 - \beta_i)$ 这个原理是说,假如我们已知 $x_0$ (即输入的图像),由于我们整个 add noise 的过程是一个线性高斯马尔科夫链,假如我们用 $x_1: x_{T}$ 来表示中间步的结果,那么: $$ q(x_1:x_T|x_0) = q(x_1|x_0) q(x_2|x_1) \dots q(x_T|x_{T- 1}) $$ 因此,我们将这个式子的 $x_i, i \in [0, T)$ 拆出来之后,就发现 $\alpha_i = \sqrt{1 - \beta_1}\sqrt{1 - \beta_2}\cdots\sqrt{1 - \beta_t}$ ### Scheduler 在上文中我们提到了 $t \sim \text{Uniform} (\{1, \dots, T\})$ ,这里的 $t$ 是一个时间步。$t$ 对于 Diffusion models 非常关键,因为其控制**随时间演化噪声的分配方式**。 常见的 schedule 有: - Linear - Cosine (噪声增加得更平滑) - 自适应 schedule(后来改进的,基于信噪比设计) 这里给出一个为什么 schedule 关键的解释。schedule 使得: - 不同时间步的信噪比分布合理; - 模型能在全程学到有用的去噪任务; - 反向采样过程稳定,最终生成质量高。 ## Reverse Process 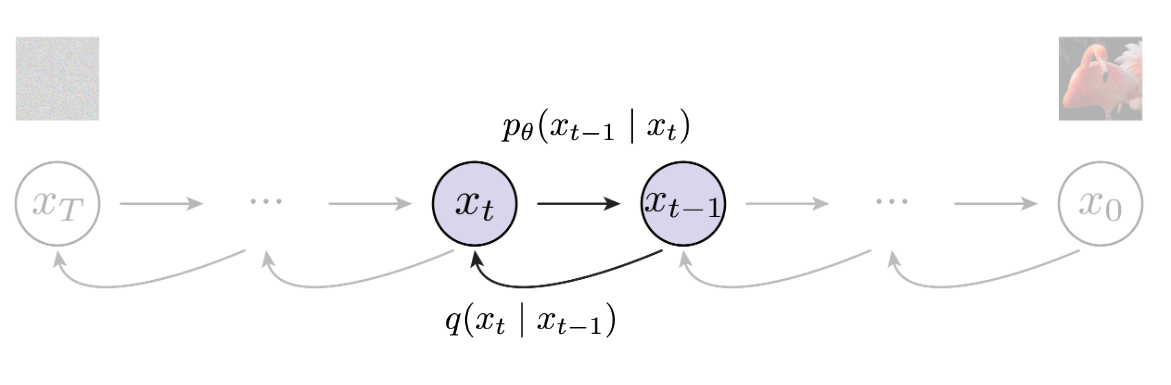 ### Definition 我们现在的目标是要学习一个反向马尔科夫链: $$ p_{\theta}(x_{t-1}|x_t), t = T, T - 1, \dots, 1 $$ 使得: $$ p_{\theta}(x_{0:T}) = p(x_T) \prod_{t=1}^{T} p_{\theta}(x_{t-1}|x_t) $$ 其中,$p(x_T) \sim \mathcal{N}(0, \mathbf{I})$ 我们有 Forward Process 的式子(线性高斯马尔可夫链),我的理解是:相当于一个有先验概率得后验概率。那么 Reverse Process 就是一个 Bayes 公式(因为我们是要从 $x_{t}$ 推导 $x_{t-1}$。那么有: $$ q(x_{t - 1} | x_t, x_0) = \mathcal{N}(x_{t-1}; \tilde{\mu_t}(x_t, x_0), \tilde{\beta_t}\mathbf{I}) $$ 其中: $$ \tilde{\mu_t} = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha_{t-1}})}{1 - \bar{\alpha_t}} x_t + \frac{\sqrt{\bar{\alpha_{t-1}}} \beta_t}{1 - \bar{\alpha_t}}x_0 $$ $$ \tilde{\beta_t} = \frac{1 - \bar{\alpha_{t-1}}}{1 - \bar{\alpha_{t}}} \beta_t $$ 这里面大概是涉及多个高斯分布的联合分布的推导,具体不展开了。比较神秘。DDPM 的附录里面有提到。在此不多赘述。 解释: - $\tilde{\mu}_t$ 是反向高斯分布的均值,由当前 noisy 样本 $x_t$ 和真实干净样本 $x_0$ 决定。 - $\tilde{\beta}_t$ 是方差,依赖于 schedule。 问题是:**反向过程需要 $x_0$,但生成时我们并不知道 $x_0$**。 ### Learn a Distribution 因此,Diffusion **会训练一个用以预测整体噪声的网络 $\epsilon_{\theta}(x_t, t)$**,这里就再次体现了时间步 $t$ 的重要性。因为 $t$ 是被当做参数一起传入 $\epsilon_{\theta}$ 中的。 根据 Forward Process ,移项可得: $$ x_0 \approx \frac{1}{\sqrt{\bar{\alpha_t}}} (x_t - \sqrt{1 - \bar{\alpha_t}}\epsilon_{\theta}(x_t, t)) $$ 再把这个 $x_0$ 代入 $\tilde{\mu_t}$ 中,就得到了反向分布的近似均值: $$ \mu_{\theta}(x_t, t) = \frac{1}{\sqrt{\alpha_t}} \left(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_{\theta}(x_t, t) \right) $$ 因此,最终的 $p_{\theta}(x_{t-1}|x_t)$ 就可以表示为: $$ p_{\theta}(x_{t-1}|x_t) = \mathcal{N} (x_{t-1}; \mu_{\theta}(x_t, t), \tilde{\beta}_t\mathbf{I}) $$ ### Train Loss 论文中有提到如何转换成 ELBO 形式。由于过于复杂,中间的主要步骤是通过类似于累乘过程中分母分子抵消来花间,这里不过多赘述。这里主要展示最后的结果: $$ \mathcal{L} = \mathbb{E}_{x_0, t, \epsilon} \left[ || \epsilon - \epsilon_{\theta} (x_t, t) ||^2\right] $$ Loading... ## 总结 Diffusion 的操作其实非常简单,核心算法的框架伪代码如下图所示:  其中 `Training` 的部分,主要包含了 **Add Noise** 这个步骤(Forward Process)。每次我们选取一张图 $x_0$ (真值),一个 $[1, T]$ 的数 $t$,和一个高斯噪声 $\epsilon \sim \mathcal{N}(0, I)$ 。每次把高斯噪声 $\epsilon$ 加给 $x_0$ 的步骤就是 add noise。**一个比较精巧(奇妙)的操作时这个 $t$**。当然,如果从 Autoregressive 的角度来看待 Diffusion,这个 $t$ 是非常合理的。 在 `Sampling` 部分,主要是包含了一个 **Denoise** 的步骤 (Reverse Process)。其中,一个用以预测整体噪声的网络 $\epsilon_{\theta}$ 是我们优化的目标。$\epsilon_{\theta}$ 要生成在 `Training` 阶段对应位置加过噪声的图片中,**真实的噪声分布**。我们**不可以把 Denoise** 简单的看成是一个 add noise 的逆过程。原因有两点: 1. Denoise 过程中消去的噪声是 $\epsilon_{\theta}$ 的预测值而非真实值。 2. 注意到 `Sampling` 阶段的末尾加上了一个神秘 $\sigma_t\mathbf{z}$。这个东西非常有说法。在这里我想提供李宏毅老师课中的一个解释。以 GPT 为例,如果预测的下一个位置永远是 Confidence 最高的 candidate,那么生成出来的文本很有可能是一段不断重复一个意思的段落。因此,LLM 中也会类似地加上一个这样的随机噪声。同理可得,如果没有在 denoise 阶段加上这个随机噪声,那么我们生成的图像可能是一张单一颜色的图像。 因此对于 denoise 过程,我目前的理解是:由于真实的图像的噪声可必然是一个**比我们目前假设的噪声分布——即高斯分布,更加复杂的分布。** 因此,Diffusion 的 denoise 实际上是在产生一个其噪声符合一个低级(简单)分布的图像。 ## Add Noise  ### Definition 在 DDPM(Denoising Diffusion Probabilistic Models)中,前向过程定义为一个 **马尔科夫链**: $$ q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t\mathbf{I}) $$ 其中: - $\beta_t$ 是一个噪声方差的超参数(通常很小,且逐渐变小) - 条件分布是高斯分布,均值缩小原输入,方差是 $\beta_t$ 也就是说,每次我们加上去一个高斯噪声 $\epsilon \sim \mathcal{N}(0, \mathbf{I})$ 给 $x_{t}$: $$ x_t = \sqrt{1 - \beta_t} x_{t - 1} + \beta_t\epsilon $$ 从这个式子我们可以看出: - **均值**:$\sqrt{1 - \beta_t} x_{t - 1}$,表示对输入的逐步衰减。 - **方差**: $\beta_t$ ,表示每一步加的高斯噪声强度。 这样设计的好处是:**整个过程可以解析化地推出任意 $t$ 时刻的分布:** $$ q(x_t|x_0) = \mathcal{N}(\sqrt{\bar{\alpha_t}}x_0, (1 - \bar{\alpha_t})\mathbf{I}) $$ 其中:$\bar{\alpha_t} = \prod_{i = 1}^{t} (1 - \beta_i)$ 这个原理是说,假如我们已知 $x_0$ (即输入的图像),由于我们整个 add noise 的过程是一个线性高斯马尔科夫链,假如我们用 $x_1: x_{T}$ 来表示中间步的结果,那么: $$ q(x_1:x_T|x_0) = q(x_1|x_0) q(x_2|x_1) \dots q(x_T|x_{T- 1}) $$ 因此,我们将这个式子的 $x_i, i \in [0, T)$ 拆出来之后,就发现 $\alpha_i = \sqrt{1 - \beta_1}\sqrt{1 - \beta_2}\cdots\sqrt{1 - \beta_t}$ ### Scheduler 在上文中我们提到了 $t \sim \text{Uniform} (\{1, \dots, T\})$ ,这里的 $t$ 是一个时间步。$t$ 对于 Diffusion models 非常关键,因为其控制**随时间演化噪声的分配方式**。 常见的 schedule 有: - Linear - Cosine (噪声增加得更平滑) - 自适应 schedule(后来改进的,基于信噪比设计) 这里给出一个为什么 schedule 关键的解释。schedule 使得: - 不同时间步的信噪比分布合理; - 模型能在全程学到有用的去噪任务; - 反向采样过程稳定,最终生成质量高。 ## Reverse Process  ### Definition 我们现在的目标是要学习一个反向马尔科夫链: $$ p_{\theta}(x_{t-1}|x_t), t = T, T - 1, \dots, 1 $$ 使得: $$ p_{\theta}(x_{0:T}) = p(x_T) \prod_{t=1}^{T} p_{\theta}(x_{t-1}|x_t) $$ 其中,$p(x_T) \sim \mathcal{N}(0, \mathbf{I})$ 我们有 Forward Process 的式子(线性高斯马尔可夫链),我的理解是:相当于一个有先验概率得后验概率。那么 Reverse Process 就是一个 Bayes 公式(因为我们是要从 $x_{t}$ 推导 $x_{t-1}$。那么有: $$ q(x_{t - 1} | x_t, x_0) = \mathcal{N}(x_{t-1}; \tilde{\mu_t}(x_t, x_0), \tilde{\beta_t}\mathbf{I}) $$ 其中: $$ \tilde{\mu_t} = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha_{t-1}})}{1 - \bar{\alpha_t}} x_t + \frac{\sqrt{\bar{\alpha_{t-1}}} \beta_t}{1 - \bar{\alpha_t}}x_0 $$ $$ \tilde{\beta_t} = \frac{1 - \bar{\alpha_{t-1}}}{1 - \bar{\alpha_{t}}} \beta_t $$ 这里面大概是涉及多个高斯分布的联合分布的推导,具体不展开了。比较神秘。DDPM 的附录里面有提到。在此不多赘述。 解释: - $\tilde{\mu}_t$ 是反向高斯分布的均值,由当前 noisy 样本 $x_t$ 和真实干净样本 $x_0$ 决定。 - $\tilde{\beta}_t$ 是方差,依赖于 schedule。 问题是:**反向过程需要 $x_0$,但生成时我们并不知道 $x_0$**。 ### Learn a Distribution 因此,Diffusion **会训练一个用以预测整体噪声的网络 $\epsilon_{\theta}(x_t, t)$**,这里就再次体现了时间步 $t$ 的重要性。因为 $t$ 是被当做参数一起传入 $\epsilon_{\theta}$ 中的。 根据 Forward Process ,移项可得: $$ x_0 \approx \frac{1}{\sqrt{\bar{\alpha_t}}} (x_t - \sqrt{1 - \bar{\alpha_t}}\epsilon_{\theta}(x_t, t)) $$ 再把这个 $x_0$ 代入 $\tilde{\mu_t}$ 中,就得到了反向分布的近似均值: $$ \mu_{\theta}(x_t, t) = \frac{1}{\sqrt{\alpha_t}} \left(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}} \epsilon_{\theta}(x_t, t) \right) $$ 因此,最终的 $p_{\theta}(x_{t-1}|x_t)$ 就可以表示为: $$ p_{\theta}(x_{t-1}|x_t) = \mathcal{N} (x_{t-1}; \mu_{\theta}(x_t, t), \tilde{\beta}_t\mathbf{I}) $$ ### Train Loss 论文中有提到如何转换成 ELBO 形式。由于过于复杂,中间的主要步骤是通过类似于累乘过程中分母分子抵消来花间,这里不过多赘述。这里主要展示最后的结果: $$ \mathcal{L} = \mathbb{E}_{x_0, t, \epsilon} \left[ || \epsilon - \epsilon_{\theta} (x_t, t) ||^2\right] $$ 最后修改:2025 年 09 月 03 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 1 如果觉得我的文章对你有用,请随意赞赏