## 前言 乱扯几句,最近发现 Anything + 生成式 还是有许多工作可以做的,算是一片蓝海吧。虽然感觉自己做什么都比别人慢几拍,前两年追热点死活追不上,不过也不能完全这么说,因为刚进大学时还屁都不懂呢。3DGS是2023年的文章,Diffusion 甚至比 GPT 要早一年(2022)就在学术圈火爆了。 离开学还有一段时间,打算慢慢补一些生成式相关的知识。遂写下一些笔记,纯当是自己在这个世界存在的证明。 ## Motivation 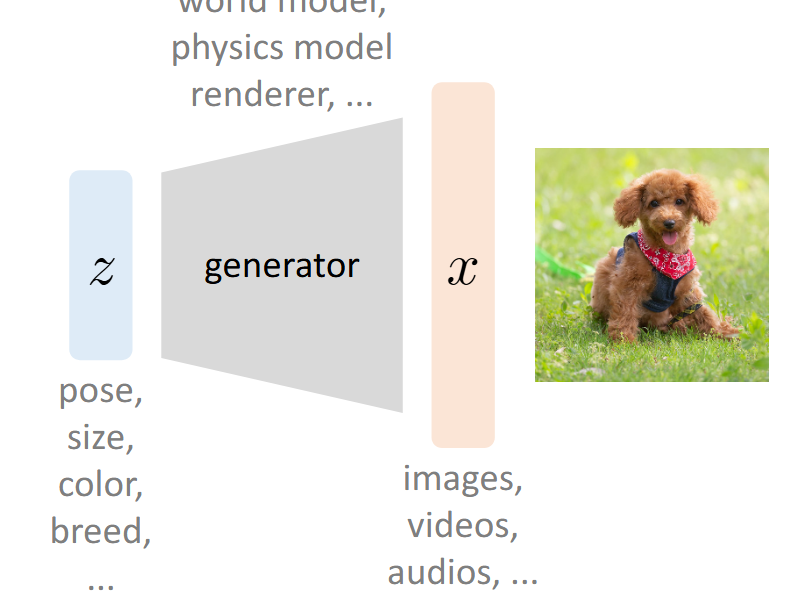 如果我们有一个这样的 Data Generation 的过程,其中我们给 Generator 的输入是一个 Latent Vector (Embedding) $z$,最终输出的是图像/视频/音频之类的数据,记为 $x$ ## Process 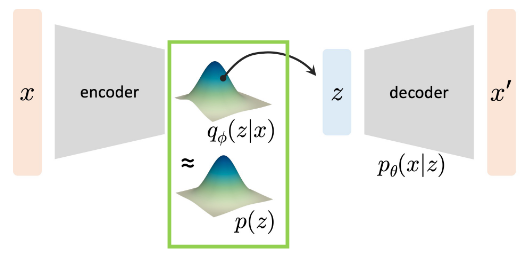 假设: - 给定的所有训练数据 $x$ 构成的分布记为 $p_{data}$ - 所有的 Latent Vectors $z_i$ 构成的分布为 $q(z)$,即:$z_i \sim q(z)$,其中 $p(z_i)$ 指的是从这个分布中 sample 到 $z_i$ 的概率密度。 - 最终的生成结果 $x' = p_{\theta}(x|z)$ - 记所有的 $x'$ 构成的分布为 $p_{\theta}(x)$,其中 $\theta$ 为 Decoder 的 Learnable Parameters 我们最终的训练目标,是 $p_{\theta}$ 接近 $p_{data}$ 的分布。我们希望用一个量化的指标来衡量两个分布的接近程度,此处选择 KL-Divergence > Question: 是否有别的 Metrics? 形式化地,我们的目标为: $$ \min_{\theta} D_{KL}(P_{data} || P_{\theta}) $$ 我们的训练目标 $\theta$ 即为: $$ \begin{align} & \arg\min_{\theta} D_{KL}(P_{data} || P_{\theta}) \\ = & \arg\min_{\theta} \sum_{x} P_{data}(x) \log(\frac{P_{data}(x)}{P_{\theta}(x)}) \\ = & \arg\min_{\theta} \sum_{x} -P_{data}(x) \log P_{\theta}(x) + C \\ = & \arg\max_{\theta} \sum_{x} \log P_{\theta}(x) \\ = & \arg\max_{\theta} \mathbb{E}_{x \sum P_{data}(x)} \log P_{\theta}(x) \end{align} $$ 其中,很明显 $P_{data}$ 是我们已知的(训练集已知),因此完全不与 $P_{\theta}$ 相关的项都写成一个常数 $C$。进一步地,由于我们此处只关心 $\theta$ ,因此 $-P_{data}(x)$ 也可以视为一个常系数。 现在我们只关心 $P_{\theta}(x)$,由于其全部由条件概率 $P_{\theta}(x|z)$ 给出,由全概率公式: $$ P_{\theta}(x) = \int_z P_{\theta}(x|z)P(z)\mathrm{d}z $$ 回到主题,我们现在的麻烦是计算 $\log P_{\theta}(x)$,我们有: $$ \begin{align} \log P_{\theta}(x) & = \int_z \log P_{\theta}(x) q(z) \mathrm{d}z \\ & = \int_z \log \left( \frac{P_{\theta}(x|z)P_{\theta}(z)}{P_{\theta}(x)} \right) q(z) \mathrm{d}z \\ & = \int_z \log \left( \frac{P_{\theta}(x|z)P_{\theta}(z)}{P_{\theta}(x)} \cdot \frac{q(z)}{q(z)}\right) q(z) \mathrm{d}z \\ & = \int_z \left( \log P_{\theta}(x|z)+ \log(\frac{P_{\theta}(z)}{q(z)}) + \log(\frac{q(z)}{P_{\theta}(z|x)}) \right) q(z) \mathrm{d}z \\ & = \mathbb{E}_{z \sim q(z)} \left[ \log P_{\theta}(x|z) \right] - D_{KL}\left(q(z) || P_{\theta}(z)\right) + D_{KL}\left( q(z) || P_{\theta}(z|x) \right) \end{align} $$ 注意第三步用到了一个很经典的 $\cdot 1$ 的技巧,此处是为了避免拆 log 的时候相关变量无法分离(导致 +/- 和括号同时产生的大混乱情况)+ 与外面的 $q(z)$ 写成 KL-散度。 我们称 Evidence Lower Bound: $$ RHS = \text{ELBO} = \mathbb{E}_{z \sim q(z)} \left[ \log P_{\theta}(x|z) \right] - D_{KL}\left(q(z) || P_{\theta}(z)\right) $$ 原因很显然,最后一项通过移项到 LHS 后显然会出现一个 $\log P_{\theta}(x)$ 的下界的形式: $$ LHS =\log P_{\theta}(x) -D_{KL}\left( q(z) || P_{\theta}(z|x) \right) $$ 观察到:LHS 中的 $\log P_{\theta}(x)$ 显然是无法计算的(不然根本没有这么些步骤),$P_{\theta}(z|x)$ 这个后验概率的分布显然也是无法表示的。那么希望寄托在 ELBO 身上。 此外,另一个关键的问题是,$z$ 作为一个 Embedding 具有以下特征: - **$z$ 会是一个高维向量** - **$q(z)$ 无法量化计算** 因此,我们引入了 **Latent Variable Models**,也就是**变分自编码器**的由来。既然我们无法确定一个“真”的 $q(z)$,如果我们可以让一个 $q_{\phi}(z|x)$ 输出一个“可控的”结果作为 $q(z)$ 的 PDF 的值,那么这个结果是可以接受的。 我们可以将期望项视作一个 Reconstruction Loss 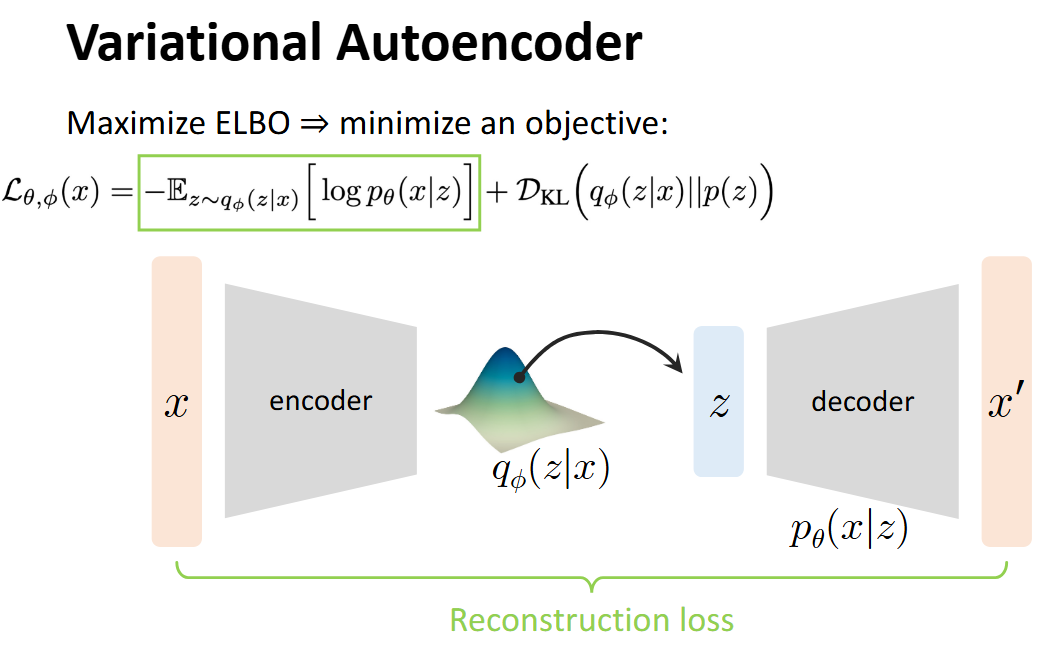 由于我们将 $q(z)$ 认为是可以近似为一个 Learnable Distribution $q_{\phi}(z|x)$ ,其中 $\phi$ 是学习的参数,那么后一项可以视为一个 Regularization Loss。其鼓励 $\phi$ 导出的网络表示的分布与真实的 $q(z)$ 越来越接近。 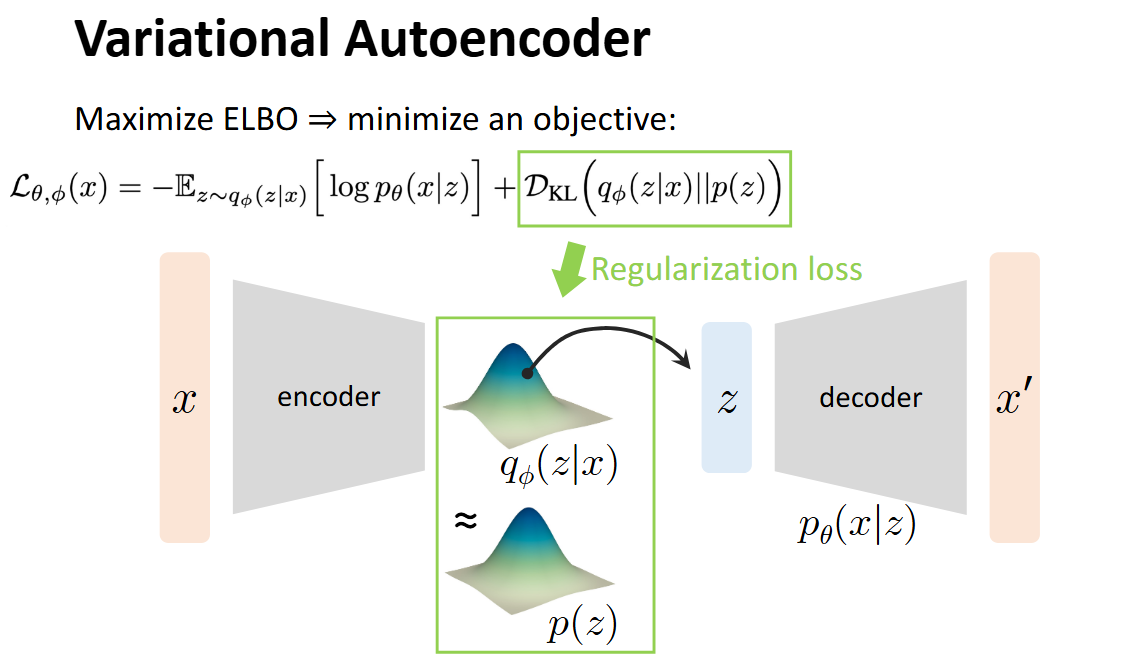 至此,整个流程就结束了。下面我们来具体关注这两个 Loss 的实现细节。 由于 Reconstruction Loss 和 Regularization Loss 的方法是一样的,下面以 Reconstruction Loss 为例。 我们关注的是: $$ - \mathbb{E}_{z \sim q(z)} \left[ \log P_{\theta}(x|z) \right] $$ 我们现在已经用一个**易采样的**近似分布:$q_{\phi}(z|x)$ 了,这里的 $\phi$ 导出的网络通常会输出分布的参数,比如说是 Gaussian 的话,那么就输出 $\mu$ 和 $\sigma$: $$ q_{\phi}(z|x) = \mathcal{N}(\mu_{\phi}(x), \sigma^2_{\phi}(x)I) $$ 这样的好处是: - 我们可以直接采样 $z^{(i)} \sim q_{\phi}(z|x)$ - 采到的 $z$ 可以直接输入生成网络 $P_\theta$ 去算概率 由此,这个期望就可以用 One-Step Monte Carlo 法计算: 1. 采样 $z^{(i)}$ 2. 用生成网络 $P_{\theta}$ 计算 $\log (P_{\theta}(x, z^{(i)}))$: - 由于:$P(x, z^{(i)}) = P(x) \cdot P(z^{(i)})$ 3. 再计算 $\log q_{\phi} (z^{(i)}|x)$ 4. 用平均值近似期望 现在的问题是,由于 $\phi$ 导出的分布参数是抖动的(即 $z$ 是取决于 $\mu_{\phi}$ 和 $\sigma_{\phi}$ 生成的),但这个采样操作里有噪声,**计算梯度时不能直接对采样过程求导**,反向传播会断掉。 这里我们就要用到一个技巧:**重参数化**。具体地,把采样过程重写为“可导的确定性变换 + 独立噪声”: 1. 先采一个与参数无关的随机变量:$\epsilon \sim \mathcal{N}(0, I)$ 2. 再用可导的线性变换得到 $z$: $$ z = \mu_{\phi}(x) + \sigma_{\phi}(x) \odot \epsilon $$ 这样的话: - 随机性来自于 $\epsilon$ - $\mu_{\phi}$ 和 $\sigma_{\phi}$ 直接参与计算 $z$,且过程可导 - 反向传播时,梯度可以从$ z$ 传到 $\mu_{\phi}$ 和 $\sigma_{\phi}$ ,从而更新 encoder 参数 现在得到 $z$ 以后,我们假设 $P_{\theta}(x|z)$ 是一个 Gaussian 分布: $$ P_{\theta}(x|z) = \mathcal{N}(x | \mu_{\theta}(z), \sigma^2I) $$ 接下来,使用负对数似然 (Negative Log-Likelihood, NLL) 作为损失。在 Gaussian 分布的这个假设下又有: $$ - \log P_{\theta}(x|z) = \frac{1}{2\sigma^2} ||x - \mu_{\theta}(z)||^2 + C $$ 这**等价于 L2 Loss**,常数项不影响优化。 Loading... ## 前言 乱扯几句,最近发现 Anything + 生成式 还是有许多工作可以做的,算是一片蓝海吧。虽然感觉自己做什么都比别人慢几拍,前两年追热点死活追不上,不过也不能完全这么说,因为刚进大学时还屁都不懂呢。3DGS是2023年的文章,Diffusion 甚至比 GPT 要早一年(2022)就在学术圈火爆了。 离开学还有一段时间,打算慢慢补一些生成式相关的知识。遂写下一些笔记,纯当是自己在这个世界存在的证明。 ## Motivation  如果我们有一个这样的 Data Generation 的过程,其中我们给 Generator 的输入是一个 Latent Vector (Embedding) $z$,最终输出的是图像/视频/音频之类的数据,记为 $x$ ## Process  假设: - 给定的所有训练数据 $x$ 构成的分布记为 $p_{data}$ - 所有的 Latent Vectors $z_i$ 构成的分布为 $q(z)$,即:$z_i \sim q(z)$,其中 $p(z_i)$ 指的是从这个分布中 sample 到 $z_i$ 的概率密度。 - 最终的生成结果 $x' = p_{\theta}(x|z)$ - 记所有的 $x'$ 构成的分布为 $p_{\theta}(x)$,其中 $\theta$ 为 Decoder 的 Learnable Parameters 我们最终的训练目标,是 $p_{\theta}$ 接近 $p_{data}$ 的分布。我们希望用一个量化的指标来衡量两个分布的接近程度,此处选择 KL-Divergence > Question: 是否有别的 Metrics? 形式化地,我们的目标为: $$ \min_{\theta} D_{KL}(P_{data} || P_{\theta}) $$ 我们的训练目标 $\theta$ 即为: $$ \begin{align} & \arg\min_{\theta} D_{KL}(P_{data} || P_{\theta}) \\ = & \arg\min_{\theta} \sum_{x} P_{data}(x) \log(\frac{P_{data}(x)}{P_{\theta}(x)}) \\ = & \arg\min_{\theta} \sum_{x} -P_{data}(x) \log P_{\theta}(x) + C \\ = & \arg\max_{\theta} \sum_{x} \log P_{\theta}(x) \\ = & \arg\max_{\theta} \mathbb{E}_{x \sum P_{data}(x)} \log P_{\theta}(x) \end{align} $$ 其中,很明显 $P_{data}$ 是我们已知的(训练集已知),因此完全不与 $P_{\theta}$ 相关的项都写成一个常数 $C$。进一步地,由于我们此处只关心 $\theta$ ,因此 $-P_{data}(x)$ 也可以视为一个常系数。 现在我们只关心 $P_{\theta}(x)$,由于其全部由条件概率 $P_{\theta}(x|z)$ 给出,由全概率公式: $$ P_{\theta}(x) = \int_z P_{\theta}(x|z)P(z)\mathrm{d}z $$ 回到主题,我们现在的麻烦是计算 $\log P_{\theta}(x)$,我们有: $$ \begin{align} \log P_{\theta}(x) & = \int_z \log P_{\theta}(x) q(z) \mathrm{d}z \\ & = \int_z \log \left( \frac{P_{\theta}(x|z)P_{\theta}(z)}{P_{\theta}(x)} \right) q(z) \mathrm{d}z \\ & = \int_z \log \left( \frac{P_{\theta}(x|z)P_{\theta}(z)}{P_{\theta}(x)} \cdot \frac{q(z)}{q(z)}\right) q(z) \mathrm{d}z \\ & = \int_z \left( \log P_{\theta}(x|z)+ \log(\frac{P_{\theta}(z)}{q(z)}) + \log(\frac{q(z)}{P_{\theta}(z|x)}) \right) q(z) \mathrm{d}z \\ & = \mathbb{E}_{z \sim q(z)} \left[ \log P_{\theta}(x|z) \right] - D_{KL}\left(q(z) || P_{\theta}(z)\right) + D_{KL}\left( q(z) || P_{\theta}(z|x) \right) \end{align} $$ 注意第三步用到了一个很经典的 $\cdot 1$ 的技巧,此处是为了避免拆 log 的时候相关变量无法分离(导致 +/- 和括号同时产生的大混乱情况)+ 与外面的 $q(z)$ 写成 KL-散度。 我们称 Evidence Lower Bound: $$ RHS = \text{ELBO} = \mathbb{E}_{z \sim q(z)} \left[ \log P_{\theta}(x|z) \right] - D_{KL}\left(q(z) || P_{\theta}(z)\right) $$ 原因很显然,最后一项通过移项到 LHS 后显然会出现一个 $\log P_{\theta}(x)$ 的下界的形式: $$ LHS =\log P_{\theta}(x) -D_{KL}\left( q(z) || P_{\theta}(z|x) \right) $$ 观察到:LHS 中的 $\log P_{\theta}(x)$ 显然是无法计算的(不然根本没有这么些步骤),$P_{\theta}(z|x)$ 这个后验概率的分布显然也是无法表示的。那么希望寄托在 ELBO 身上。 此外,另一个关键的问题是,$z$ 作为一个 Embedding 具有以下特征: - **$z$ 会是一个高维向量** - **$q(z)$ 无法量化计算** 因此,我们引入了 **Latent Variable Models**,也就是**变分自编码器**的由来。既然我们无法确定一个“真”的 $q(z)$,如果我们可以让一个 $q_{\phi}(z|x)$ 输出一个“可控的”结果作为 $q(z)$ 的 PDF 的值,那么这个结果是可以接受的。 我们可以将期望项视作一个 Reconstruction Loss  由于我们将 $q(z)$ 认为是可以近似为一个 Learnable Distribution $q_{\phi}(z|x)$ ,其中 $\phi$ 是学习的参数,那么后一项可以视为一个 Regularization Loss。其鼓励 $\phi$ 导出的网络表示的分布与真实的 $q(z)$ 越来越接近。  至此,整个流程就结束了。下面我们来具体关注这两个 Loss 的实现细节。 由于 Reconstruction Loss 和 Regularization Loss 的方法是一样的,下面以 Reconstruction Loss 为例。 我们关注的是: $$ - \mathbb{E}_{z \sim q(z)} \left[ \log P_{\theta}(x|z) \right] $$ 我们现在已经用一个**易采样的**近似分布:$q_{\phi}(z|x)$ 了,这里的 $\phi$ 导出的网络通常会输出分布的参数,比如说是 Gaussian 的话,那么就输出 $\mu$ 和 $\sigma$: $$ q_{\phi}(z|x) = \mathcal{N}(\mu_{\phi}(x), \sigma^2_{\phi}(x)I) $$ 这样的好处是: - 我们可以直接采样 $z^{(i)} \sim q_{\phi}(z|x)$ - 采到的 $z$ 可以直接输入生成网络 $P_\theta$ 去算概率 由此,这个期望就可以用 One-Step Monte Carlo 法计算: 1. 采样 $z^{(i)}$ 2. 用生成网络 $P_{\theta}$ 计算 $\log (P_{\theta}(x, z^{(i)}))$: - 由于:$P(x, z^{(i)}) = P(x) \cdot P(z^{(i)})$ 3. 再计算 $\log q_{\phi} (z^{(i)}|x)$ 4. 用平均值近似期望 现在的问题是,由于 $\phi$ 导出的分布参数是抖动的(即 $z$ 是取决于 $\mu_{\phi}$ 和 $\sigma_{\phi}$ 生成的),但这个采样操作里有噪声,**计算梯度时不能直接对采样过程求导**,反向传播会断掉。 这里我们就要用到一个技巧:**重参数化**。具体地,把采样过程重写为“可导的确定性变换 + 独立噪声”: 1. 先采一个与参数无关的随机变量:$\epsilon \sim \mathcal{N}(0, I)$ 2. 再用可导的线性变换得到 $z$: $$ z = \mu_{\phi}(x) + \sigma_{\phi}(x) \odot \epsilon $$ 这样的话: - 随机性来自于 $\epsilon$ - $\mu_{\phi}$ 和 $\sigma_{\phi}$ 直接参与计算 $z$,且过程可导 - 反向传播时,梯度可以从$ z$ 传到 $\mu_{\phi}$ 和 $\sigma_{\phi}$ ,从而更新 encoder 参数 现在得到 $z$ 以后,我们假设 $P_{\theta}(x|z)$ 是一个 Gaussian 分布: $$ P_{\theta}(x|z) = \mathcal{N}(x | \mu_{\theta}(z), \sigma^2I) $$ 接下来,使用负对数似然 (Negative Log-Likelihood, NLL) 作为损失。在 Gaussian 分布的这个假设下又有: $$ - \log P_{\theta}(x|z) = \frac{1}{2\sigma^2} ||x - \mu_{\theta}(z)||^2 + C $$ 这**等价于 L2 Loss**,常数项不影响优化。 最后修改:2025 年 09 月 01 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 2 如果觉得我的文章对你有用,请随意赞赏
1 条评论
暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托暴力摩托