Luogu1641 [SCOI2010]生成字符串

tony102

2021 年 06 月 12 日

1922 次浏览

暂无评论

1292字数

题解

[Link](https://www.luogu.com.cn/problem/P1641)

## Sol

这个题的方法对于一类恰好要求某个有顺序的值到达一个阀值的限制的题目是启发的

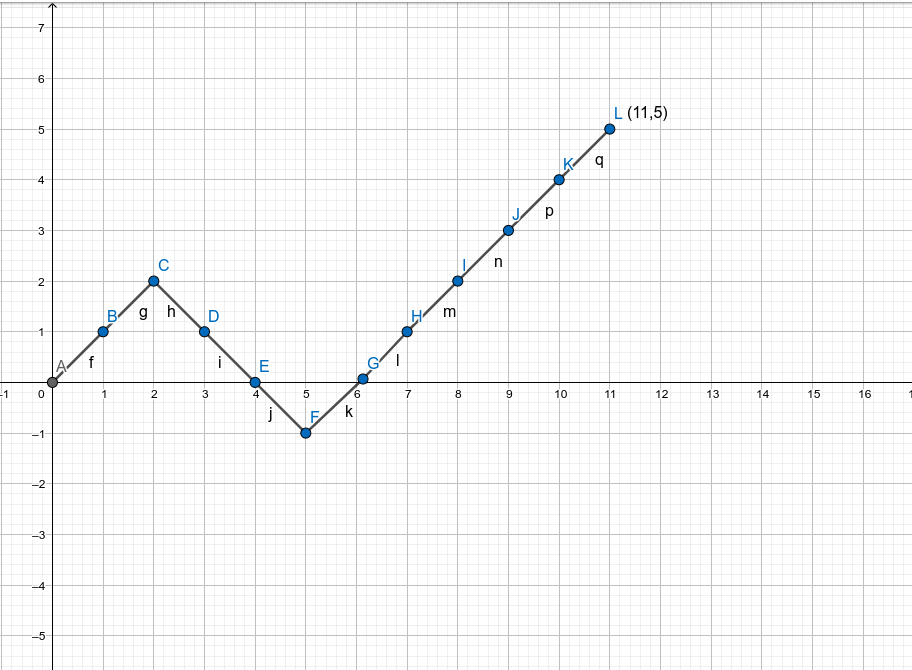[![25k1nH.png](https://tony102.com/usr/uploads/2021/09/4072506634.png)](https://imgtu.com/i/25k1nH)

用 $x$ 轴的 $+1$ 表示 $1$ 的数量与 $0$ 的数量的**和** $+1$, $y$ 轴方向的 $+1$ 表示 $1$ 的数量与 $0$ 的数量的**差** $+1$. 那么最终要求的放置的 $n$ 个 $1$ 和 $m$ 个 $0$ 就会停在图中的 $L(n + m, n - m)$ 这个点上.

从 $0$ 走到 $L(n+m,n-m)$ 的方案数可以被表示为 $\binom{n + m}{n} = \binom{n+m}{m}$ , 组合意义阐释: 我们一共要选出 $n + m$ 个 $0$ 或 $1$ , 也就是在图中走了 $n + m$ 步, 其中有 $n$ 步选了 $1$ , 就代表在图中从 $(x, y)\to (x + 1, y+1)$ ,也就是 $1$ 与 $0$ 数量的差 $+1$, 选 $0$ 则是 $(x,y) \to (x +1,y-1)$ ,就是往 $\searrow$ 方向上走了一步. 那么走到 $L(n+m,n-m)$ 这个点的方案数就是在 $n+m$ 步里面选了 $n$ 步往 $\nearrow$ 或者 $m$ 步 $\searrow$

那么再来考虑题目给的限制.题目的限制其实就是任意一个前缀一定要满足当前在图上的纵坐标要不经过 $y = -1$ 这一条线.

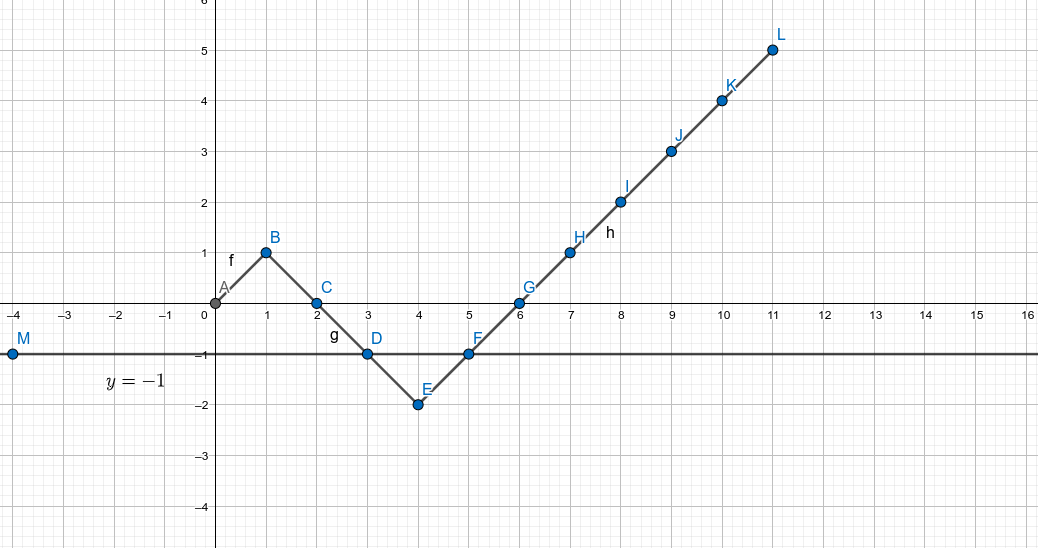[![25Afit.png](https://tony102.com/usr/uploads/2021/09/3024658736.png)](https://imgtu.com/i/25Afit)

这种经过一条直线且起点终点不在一边的都有一个方法,就是把它关于那条直线对称一下就好了

对称了之后七点到了 $(0,-2)$ ,那么从 $(0,-2)$ 走到 $(n+m,n-m)$ 这个点的方案数就是$\binom{n+m}{m-1}$

用总的方案数减掉这部分不合法的就可以了

## Code

```cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;

const int SIZE = 2e6 + 5;
const int mod = 20100403;

int n, m;
int inv[SIZE], fac[SIZE];

namespace GTR {
	const int bufl = 1 << 15;
	char buf[bufl], *s = buf, *t = buf;
	inline int fetch() {
		if (s == t) { t = (s = buf) + fread(buf, 1, bufl, stdin); if (s == t) return EOF; }
		return *s++;
	}
	inline int read() {
		int a = 0, b = 1, c = fetch();
		while (c < 48 || c > 57) b ^= c == '-', c = fetch();
		while (c >= 48 && c <= 57) a = (a << 1) + (a << 3) + c - 48, c = fetch();
		return b ? a : -a;
	}
} using GTR::read;

int qPow(int a, int b) {
	int ans = 1ll;
	for ( ; b; b >>= 1, a = a * a % mod) {
		if (b & 1) ans = ans * a % mod;
	}
	return ans % mod;
}

void init() {
	const int siz = n + m;
	fac[0] = fac[1] = 1ll;
	for (int i = 2; i <= siz; ++ i) fac[i] = fac[i - 1] * i % mod;
	inv[siz] = qPow(fac[siz], mod - 2ll);
	for (int i = siz - 1; ~i; -- i) inv[i] = inv[i + 1] * (i + 1ll) % mod;
}

int C(int x, int y) {
	return x < y ? 0ll : fac[x] * inv[y] % mod * inv[x - y] % mod;
}

signed main() {
	// freopen("code.in", "r", stdin);
	n = read(), m = read(); init();
	printf("%lld\n", (C(n + m, m) - C(n + m, m - 1) + mod) % mod);
	return 0;
}
```

最后修改：2021 年 09 月 07 日