TOC Final Review

## Lec 7 CFG

### PDA

形式化定义：A **pushdown automaton** is a 6-tuple
$$
(Q, \Sigma, \Gamma, \delta, q_0, F),
where:
$$

- $Q$ is the finite set of states;
- $\Sigma$ is the finite input alphabet;
- $\Gamma$ is the finite stack alphabet;
- $\delta : Q \times \Sigma_{\varepsilon} \times \Gamma_{\varepsilon} \rightarrow \mathcal{P}(Q \times \Gamma_{\varepsilon})$ is the transition function;
- $q_0 \in Q$ is the initial state; and
- $F \subseteq Q$ is the set of final states.

#### Problem 1： 设计 PDA

一些比较基本的经验和操作。

对于栈操作来说，比如是 $op_a \to op_b$ 代表当前栈顶是 $op_a$，将栈顶变为 $op_b$。那么这个意思就比较丰富了：

1. 若形如：$a \to b$，其中 $a, b \in L$（就是说现在在栈里面要匹配的字符属于当前language的字符集），那么实际上的意思是 `pop(a) + push(b)`，相当于是用 $b$ 替换当前栈顶的元素 $a$。
2. 若形如：$\epsilon \to b$， 意思是 `push(b)`。因为 $\epsilon$ 是要匹配一个空。
3. 若形如：$b \to \epsilon$，意思是 `pop(b)`，其中 $b$ **一定是栈顶元素！！！！**。要时刻记得 $op_a$ 是栈顶元素。

下面是一些常见的设计PDA需要的栈操作：

1. $\epsilon \to \$$ **一定要加！**： 这一步是为了让一个空的栈有一个”空“的标记 （即 $\$$ ）
2. $\epsilon \to \epsilon$ ：相当于是我们不对栈进行任何操作 （见 A2-Q1-a）。**一个比较好用的东西**: $\epsilon, \epsilon \to \epsilon$ 可以用来处理 $n, m = 0$ 的 case。

##### e.g.1

$L = a^nb^{n+m}c^m$

这道题可以学习的点：注意到其实我们设计的都是NPDA，那么对于一个 $w \in L$ （属于当前language的串），我们只要 PDA 存在一个路径让他到达 Final state 即可。我们这里通过 $a, b, c$ 的标志来区分数量，**中间用 $\epsilon, \epsilon \to \epsilon$** **来转移到下一个计数 state**。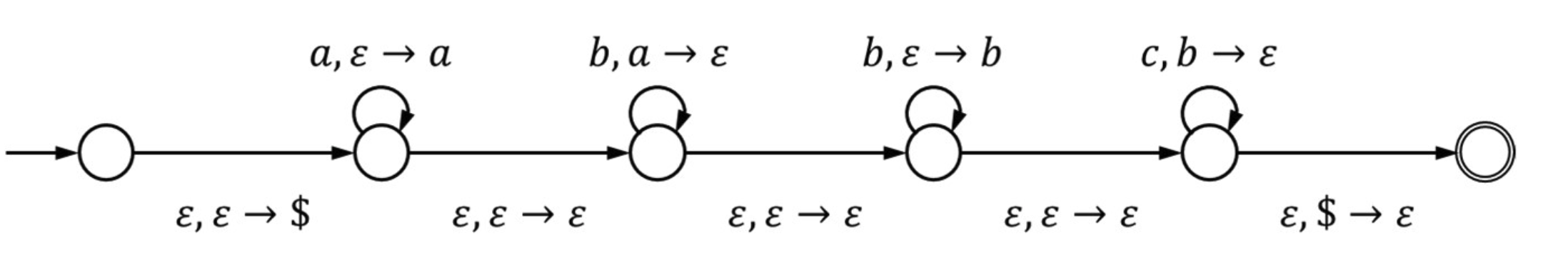

![image](https://img.tony102.com/i/2025/12/26/rbwvxc.png)

##### e.g.2

$L = a^n b^{2n}$

这道题可以学习的点：这里需要处理的主要是 $n$ 个 a 和 $2n$ 个 b 的倍数关系。难点在于我们需要设计使得每读进来一个 $a$ 可以往栈里面 `push` 两个 $a$。实现可以参考答案。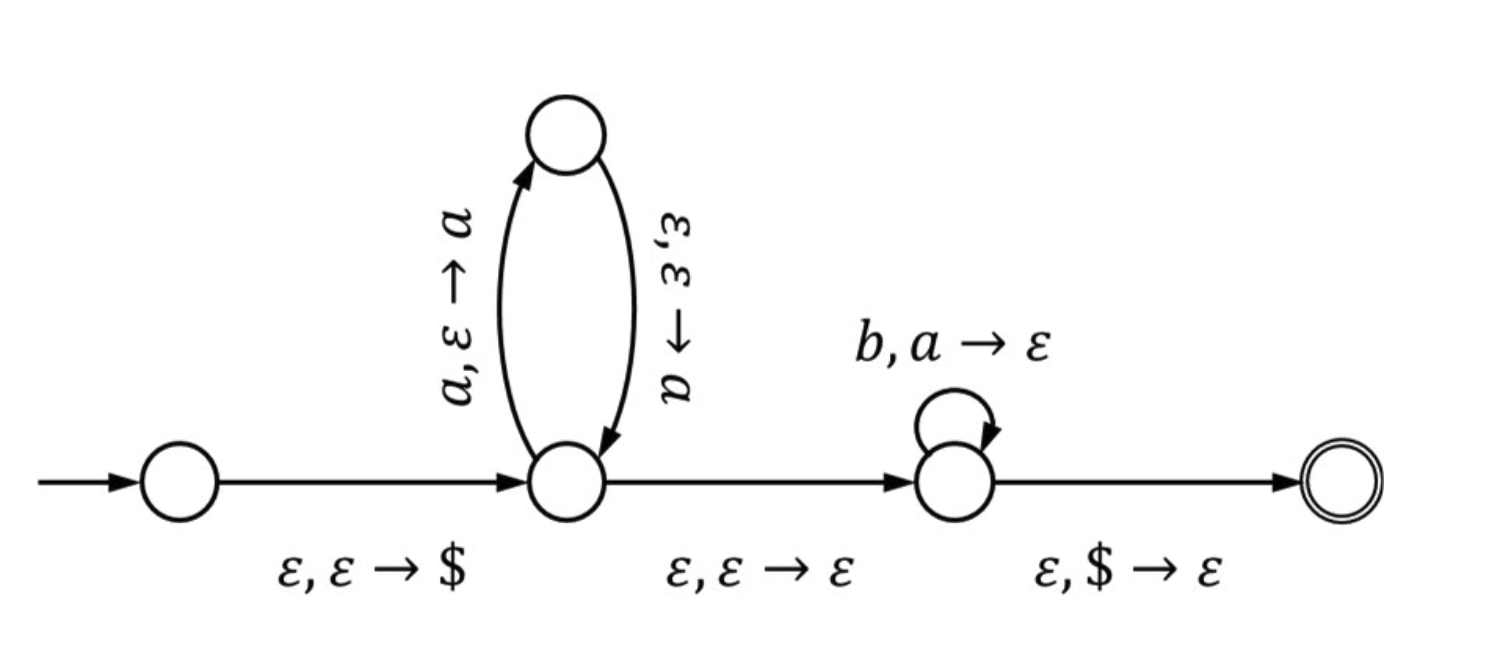

![image](https://img.tony102.com/i/2025/12/26/s4rwqq.png)

##### e.g.3

$L = a^nb^{m}c^{l}, n \geq m | n \geq l$

答案错了。权威这一块，拿捏的死死的。

一些小细节：

1. 最后进入 Final state 的时候，由于可能 $n > m | l$ ，那么 stack 里面还有剩余的 $a$，设计转移的时候要注意。 
2. 此外就是一个标准的双分支结构，用 $\epsilon, \epsilon \to \epsilon$ 转移就好。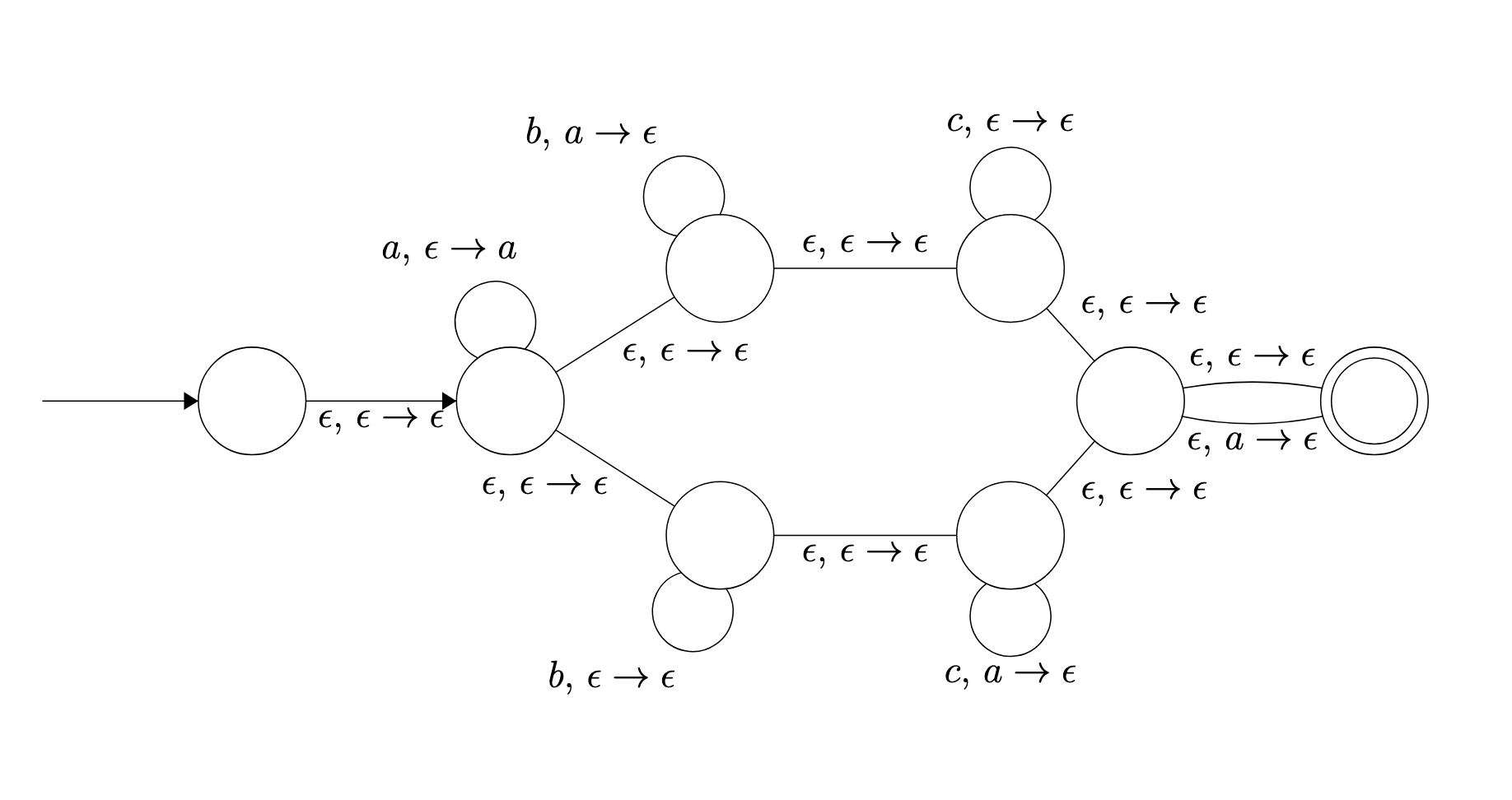

![4634d1a26a30f30c4817afe70b5aa33b](https://img.tony102.com/i/2025/12/26/sjnyf8.png)

#### Problem 2：PDA 和 CFG 的互相转换

感觉比较能出的实际上是CFG 2 PDA

比较要注意的实际上是：

| Type                      | 做法                                                         |
| ------------------------- | ------------------------------------------------------------ |
| Terminals                 | 1. 先从 $NT \to T$ （从变量推导出 Terminals）；再加入：$T \to \epsilon$  （处理完毕，出栈）; 2. 对于每一个 Terminals，都要有出栈。 |
| Non-Terminals（Recursion) | **注意一定是从右到左**；比如说有：$S \to aSb$，那么要有转移 $\epsilon, S \to b | \epsilon \to S | \epsilon \to a$ |

最后一定要加入 $\epsilon, \$ \to \epsilon$ 到 final state 的转移。

放个作业题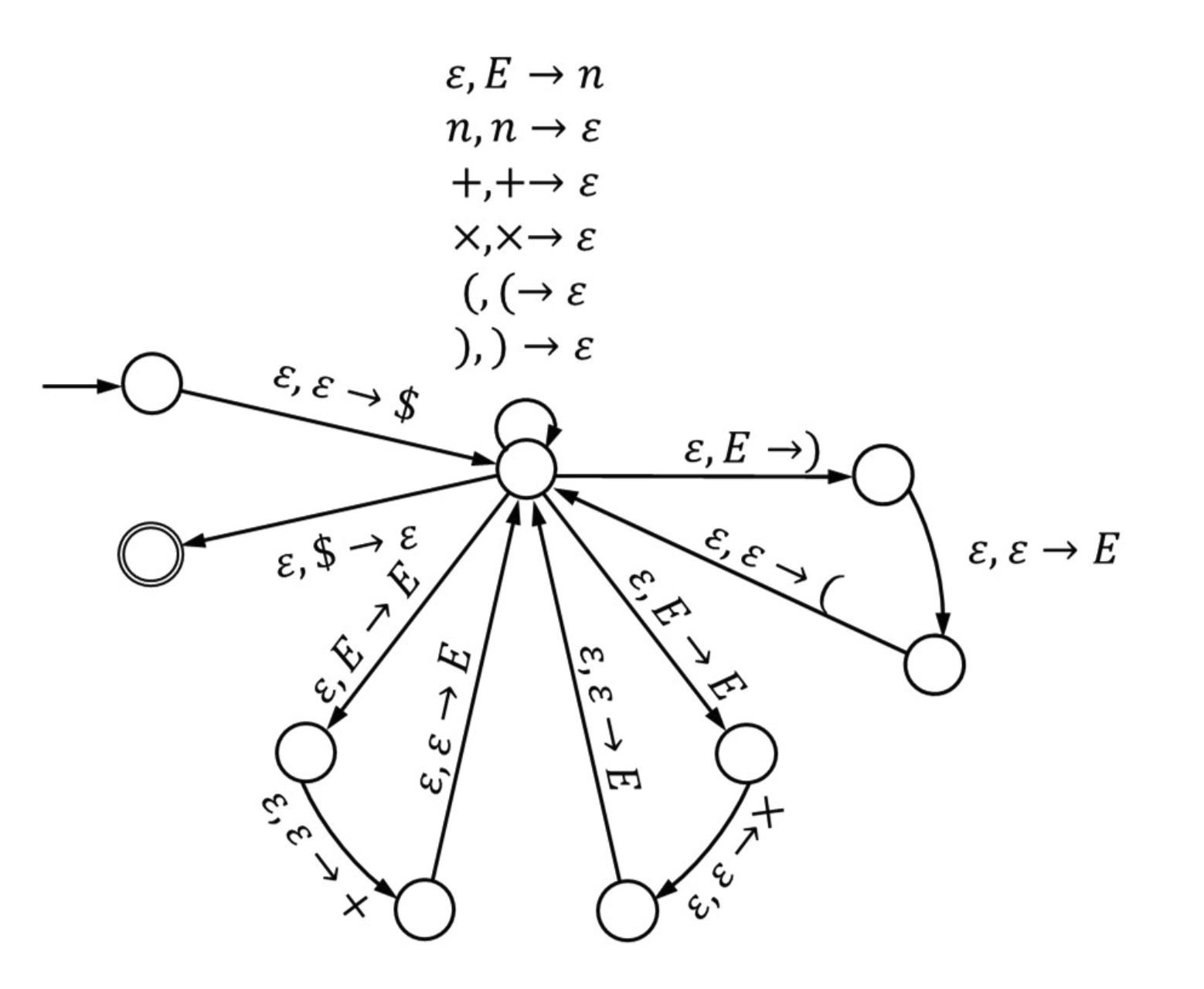

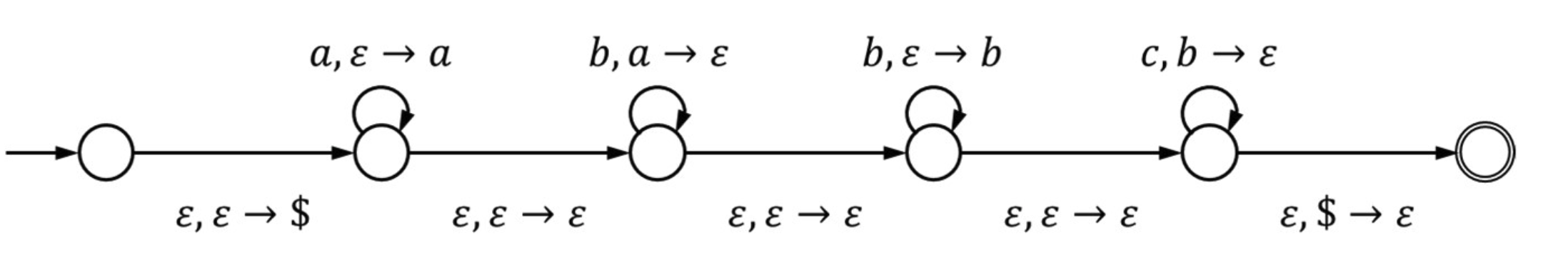![image](https://img.tony102.com/i/2025/12/26/xsip5z.png)

#### Problem 3: 证明 CFG 是 ambiguous 的

Compiler 题型，做法也很简单：**找一个属于这个CFG的串，画出两棵不同的 parsing tree 即可**

### CFG Properties

感觉不是很重要，一笔带过吧

满足的性质：

1. Union: $L_1, L_2$ 都是 CFG $\Rightarrow$ $L_1 \cup L_2$ 也是 CFG
2. Concat: $L_1 \cdot L_2$ 也是 CFG
3. Star
4. 与 regular language 的交：$L_R \cup L_C$ 也是 CFG

不满足的性质：

1.  Complement

### Pumping Lemma

感觉其实会简单一些，主要是由于 CFL 的构造会复杂一些，所以枚举的case必须要覆盖全面。其他的倒是比较简单。

## Lec 9 TM

A **Turing Machine** is a 7-tuple 
$$
M = (Q, \Sigma, \Gamma, \delta, q_0, q_{\text{accept}}, q_{\text{reject}})
$$

1. $Q$ is the set of states;

2. $\Sigma$ is the input alphabet  
   $$
   \sqcup \notin \Sigma
   $$

3. $\Gamma$ is the tape alphabet  
   $$
   \sqcup \in \Gamma \quad \text{and} \quad \Sigma \subseteq \Gamma
   $$

4. The transition function is  
   $$
   \delta : Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\}
   $$

5. $q_0 \in Q$ is the start state;

6. $q_{\text{accept}} \in Q$ is the accept state; and

7. $q_{\text{reject}} \in Q$ is the reject state, where  
   $$
   q_{\text{reject}} \neq q_{\text{accept}}
   $$

感觉一些比较容易忽略的点：

1. TM **rejects** a string $w$ if
   1. it halts on the input $w$ at a reject state or
   2. it has no where to move in the middle of the process

2. **Turing-decideable**: A language $L$ is **recursive** (or Turing-decidable) if there is a TM $M$ such that
   1. $\forall w \in L$, $M$ accpets $w$;
   2. $\forall w \not \in L$, M rejects $w$
3. **Turing-recognizable**: A language $L$ is recursively enumerable (or Turing-recognizable) if there is a TM $M$ such that:
   1. $\forall w \in L$, $M$ accpets $w$;
   2. $\forall w \in L$, $M$ rejects $w$ or $M$ loops forever

#### Problem 4a: 设计 TM (Decider)

一些比较好的设计规范：

1. 要对不同字符操作的时候最好退回到纸带起点
2. 可以用不同的字母表示不同的含义，比如说 (a,b) 配对用 x，(b,c) 配对用 y 这样。

##### 类型 1: **数量倍数关系判定**

对于 $L_1  = \{a^nb^{m} | n = 2m, n \geq 0, m \geq 0\}$

设计思路：

- 参考 A3-Q1 中的 $a^ib^jc^k$
- 策略：每次划掉一个 a，然后去找一个 b，**退回到纸带最左边**，然后再划掉一个 a，最后又退回到最左边。如果 a 找不到了，就可以 accept 了

<?xml version="1.0" encoding="UTF-8"?>

##### 类型 2: **逆序结构判定（回文）**

对于 $L_2 = \{w \in \{0, 1\}^{*} | w = w^{R } \}$

设计思路：

- 读取最左边的字符，记住它是 0 还是 1（通过状态来记忆，相当于走到不同状态分支）。标记
- 然后移动到最右边未被标记的字符，检查其是否与左边的一致。如果一致，删掉右边这个字符并移回最左边；
- 注意到奇数长度的串需要特别判断：如果从右边往左边扫的时候遇到空格了，可以直接进入 acc 状态

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

##### 类型 3：加法

对于 $L_3 = \{a^ib^jc^k | i + k = j, i, j, k \geq 1\}$

设计思路：

- 可以先匹配 *a* 和 *b*。每次划掉一个 *a*，对应划掉一个 *b*。当 *a* 全部划掉后，继续匹配 *c* 和剩余的 *b*。如果 *c* 耗尽时 *b* 也刚好耗尽，则接受。

##### 类型 4: 幂次判定

对于 $L_4 = \{a^n | n = 2^k, k \geq 0\}$

设计思路：

- 通过重复“除以 2”的过程。
- 从左到右扫描，每隔一个 *a* 划掉一个 *a*（保留一半）。
-  如果扫描过程中发现总数是奇数（且总数大于1），则拒绝。
- 扫描完一轮后，将读写头移回开头，重复步骤 1。
- 如果最后只剩下一个 *a*，则接受。

#### Problem 4b: 设计 TM (Computation)

由于TM会在tape上写写画画（称之为 side effect），故可以用来做一些 computation 任务

##### 类型 1: 前驱后继

作业已经设计过一个前驱了，现在来考虑一下后继。

主要的问题都是：

- 低位在右边
- 考虑进位

设计思路：

**设计提示：**

◦ 这是 Q2x 的逆运算。你需要先将读写头移动到最右端的 LSB。

◦ 从右向左扫描：如果你看到 `1`，将其变为 `0` 并继续向左进位（Carry）；如果你看到 `0`，将其变为 `1` 并停止（进入 Halt 状态）。

◦ **边界情况：** 如果移动到最左边还是进位（例如 `11` + 1），你需要处理溢出，可能需要整体右移数据或在左边插入一个 `1`。

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

##### 类型 2: **一进制转二进制 (Unary to Binary Conversion)**

双带（2-tape）TM

设计思路：

这道题可以直接复用 **Q1** 的逻辑作为子程序（Subroutine）。

◦ **策略：** 纸带 2 作为一个计数器，初始当作 `0`。读写头在纸带 1 上每读到一个 `x`，就在纸带 2 上执行一次“加 1”操作（调用 Q1 的逻辑）。

◦ 当纸带 1 的 `x` 读完时，纸带 2 上的内容即为结果。

其他的我感觉考试也不可能出太过分了，据说去年出了一个去模，我感觉思路应该类似于辗转相除法。如果出了我就认账。

## Lec 7 CFG

### PDA

形式化定义：A **pushdown automaton** is a 6-tuple
$$
(Q, \Sigma, \Gamma, \delta, q_0, F),
where:
$$

#### Problem 1： 设计 PDA

一些比较基本的经验和操作。

对于栈操作来说，比如是 $op_a \to op_b$ 代表当前栈顶是 $op_a$，将栈顶变为 $op_b$。那么这个意思就比较丰富了：

下面是一些常见的设计PDA需要的栈操作：

##### e.g.1

$L = a^nb^{n+m}c^m$

![image](https://img.tony102.com/i/2025/12/26/rbwvxc.png)

##### e.g.2

$L = a^n b^{2n}$

![image](https://img.tony102.com/i/2025/12/26/s4rwqq.png)

##### e.g.3

$L = a^nb^{m}c^{l}, n \geq m | n \geq l$

答案错了。权威这一块，拿捏的死死的。

一些小细节：

![4634d1a26a30f30c4817afe70b5aa33b](https://img.tony102.com/i/2025/12/26/sjnyf8.png)

#### Problem 2：PDA 和 CFG 的互相转换

感觉比较能出的实际上是CFG 2 PDA

比较要注意的实际上是：

最后一定要加入 $\epsilon, \$ \to \epsilon$ 到 final state 的转移。

放个作业题

![image](https://img.tony102.com/i/2025/12/26/xsip5z.png)

#### Problem 3: 证明 CFG 是 ambiguous 的

Compiler 题型，做法也很简单：**找一个属于这个CFG的串，画出两棵不同的 parsing tree 即可**

### CFG Properties

感觉不是很重要，一笔带过吧

满足的性质：

1. Union: $L_1, L_2$ 都是 CFG $\Rightarrow$ $L_1 \cup L_2$ 也是 CFG
2. Concat: $L_1 \cdot L_2$ 也是 CFG
3. Star
4. 与 regular language 的交：$L_R \cup L_C$ 也是 CFG

不满足的性质：

1.  Complement

### Pumping Lemma

感觉其实会简单一些，主要是由于 CFL 的构造会复杂一些，所以枚举的case必须要覆盖全面。其他的倒是比较简单。

## Lec 9 TM

A **Turing Machine** is a 7-tuple 
$$
M = (Q, \Sigma, \Gamma, \delta, q_0, q_{\text{accept}}, q_{\text{reject}})
$$

1. $Q$ is the set of states;

2. $\Sigma$ is the input alphabet  
   $$
   \sqcup \notin \Sigma
   $$

3. $\Gamma$ is the tape alphabet  
   $$
   \sqcup \in \Gamma \quad \text{and} \quad \Sigma \subseteq \Gamma
   $$

4. The transition function is  
   $$
   \delta : Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\}
   $$

5. $q_0 \in Q$ is the start state;

6. $q_{\text{accept}} \in Q$ is the accept state; and

7. $q_{\text{reject}} \in Q$ is the reject state, where  
   $$
   q_{\text{reject}} \neq q_{\text{accept}}
   $$

感觉一些比较容易忽略的点：

1. TM **rejects** a string $w$ if
   1. it halts on the input $w$ at a reject state or
   2. it has no where to move in the middle of the process

#### Problem 4a: 设计 TM (Decider)

一些比较好的设计规范：

1. 要对不同字符操作的时候最好退回到纸带起点
2. 可以用不同的字母表示不同的含义，比如说 (a,b) 配对用 x，(b,c) 配对用 y 这样。

##### 类型 1: **数量倍数关系判定**

对于 $L_1  = \{a^nb^{m} | n = 2m, n \geq 0, m \geq 0\}$

设计思路：

<?xml version="1.0" encoding="UTF-8"?>

##### 类型 2: **逆序结构判定（回文）**

对于 $L_2 = \{w \in \{0, 1\}^{*} | w = w^{R } \}$

设计思路：

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

##### 类型 3：加法

对于 $L_3 = \{a^ib^jc^k | i + k = j, i, j, k \geq 1\}$

设计思路：

- 可以先匹配 *a* 和 *b*。每次划掉一个 *a*，对应划掉一个 *b*。当 *a* 全部划掉后，继续匹配 *c* 和剩余的 *b*。如果 *c* 耗尽时 *b* 也刚好耗尽，则接受。

##### 类型 4: 幂次判定

对于 $L_4 = \{a^n | n = 2^k, k \geq 0\}$

设计思路：

#### Problem 4b: 设计 TM (Computation)

由于TM会在tape上写写画画（称之为 side effect），故可以用来做一些 computation 任务

##### 类型 1: 前驱后继

作业已经设计过一个前驱了，现在来考虑一下后继。

主要的问题都是：

- 低位在右边
- 考虑进位

设计思路：

**设计提示：**

◦ 这是 Q2x 的逆运算。你需要先将读写头移动到最右端的 LSB。

◦ 从右向左扫描：如果你看到 `1`，将其变为 `0` 并继续向左进位（Carry）；如果你看到 `0`，将其变为 `1` 并停止（进入 Halt 状态）。

◦ **边界情况：** 如果移动到最左边还是进位（例如 `11` + 1），你需要处理溢出，可能需要整体右移数据或在左边插入一个 `1`。

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

##### 类型 2: **一进制转二进制 (Unary to Binary Conversion)**

双带（2-tape）TM

设计思路：

这道题可以直接复用 **Q1** 的逻辑作为子程序（Subroutine）。

◦ **策略：** 纸带 2 作为一个计数器，初始当作 `0`。读写头在纸带 1 上每读到一个 `x`，就在纸带 2 上执行一次“加 1”操作（调用 Q1 的逻辑）。

◦ 当纸带 1 的 `x` 读完时，纸带 2 上的内容即为结果。

其他的我感觉考试也不可能出太过分了，据说去年出了一个去模，我感觉思路应该类似于辗转相除法。如果出了我就认账。

最后修改：2025 年 12 月 29 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

名人传

VP: AtCoder Beginner Contest 222(ABC222)

机房标准化岚语发音对照

写在 CSP-S2021 前

VP: AtCoder Beginner Contest 221(ABC221)

CF515E Drazil and Park

ARC127D Sum of Min of Xor

CodeChef Cards, bags and coins

20211110 漂亮轰炸 (bomb)

AT2370 [AGC013D] Piling Up

TOC Final Review

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

TOC Final Review

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款