TOC Review 1: From Math Preperation to Pumping Lemma

## Lec 02: Math

好像是一些概念，先放点重要的

### Constructive Proof

**规范步骤：**

1. Used to prove a predicate with existential quantifiers, *i.e.* $\exist x, P(x)$
2. First, construct an object $x$
3. Second, prove $P(x)$ is true

## Contradiction Proof

懒得写了，大概就是：

1. 写一个命题 $\exist x, P(x)$
2. 然后给出逆否命题 $\exist \neg x$，并且证明 $P(\neg x)$ 为真
3. 自然得到 $x$ 为假

### Induction

要证明 $\forall x \in \mathbb{N}, P(x)$，一句话：**一般归纳法只要 $k \to k+1$ 就行，但是 strong induction 要求** $1 \land 2 \land 3 \land \dots \land k \to k + 1$

### Cardinality （范数）

首先抄一下定义：

![Cardinality](https://img.tony102.com/i/2025/10/19/sdo8h0.png)

![截屏2025-10-19 17.16.30](https://img.tony102.com/i/2025/10/19/sdvhz8.png)

证明 **Countable/Uncountable** 的方法主要有两个方法

1. Construct a bijection: $f: A \to \mathbb{N}$ **核心在于 Bijection**
   1. 可以是一个函数，比如你要弄到 $(0,1)$ 就可以用 sigmoid 或者其他 activation function；你要证明 $[0, 10]$ 是 uncountable 的话，**即可以说明其 subset 不可数，亦可以写一个 $f(x) = \frac{x}{10}$ 之类的**
   2. 也可以是一个可以 map to $\mathbb{N}$ 的遍历顺序
      - 如果是一个形如 $(x_i, y_i)$ 这样的二元组要给一个遍历顺序的话，可以构造 zig-zag
2. 否则的话就需要用 Diagonal Proof 了，说实话这个比较唐。相当于你要给出一个遍历表，然后想办法构造一个不存在于表中的元素来说明你要证明的集合   uncountable.

## Lec 03/04: (Non-)Finite Automata

定义：需要包含一下元素

5 tuple $(Q, \Sigma, \delta, q_0, F)$ where:

- $Q$ is a finite set of states
- $\Sigma$ is a finite set, called the alphabet (set of input symbols)
- $\delta$: $Q \times \Sigma \to Q$ is the transition function
- $q_0 \in Q$ is the start (initial) state
- $F \subseteq Q$ is the set of final (accept) states

### 做题1：设计 DFA / NFA

#### 类型1: 数量型

这类是比较简单的题型。**Solution: 设计足够的转移边来满足数量匹配即可。**

比如说：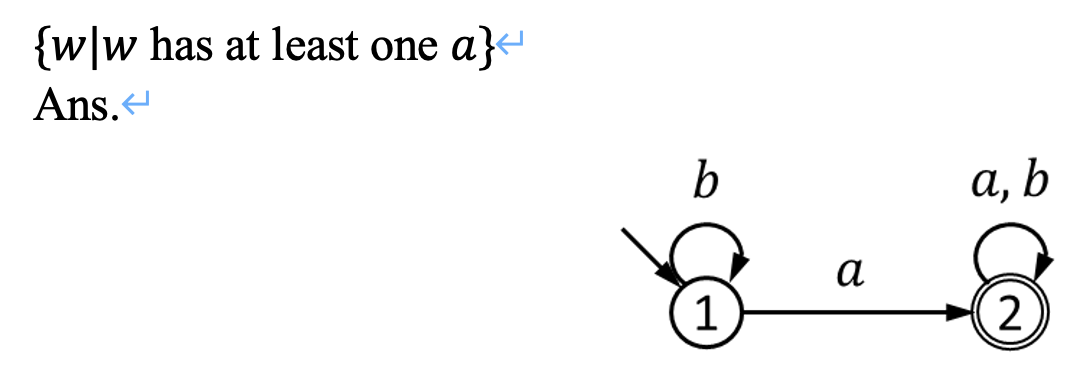

![image](https://img.tony102.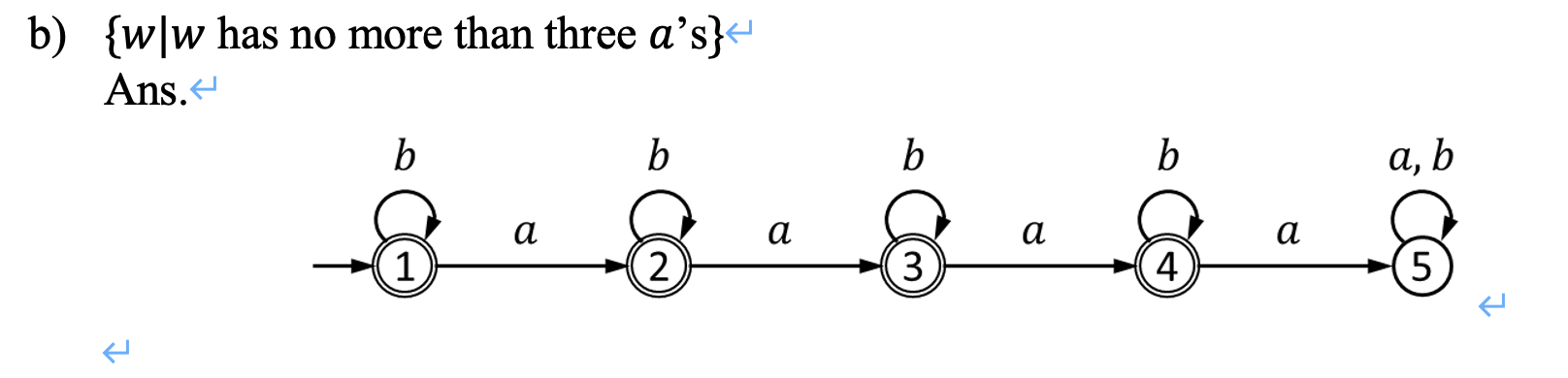com/i/2025/10/19/ul2x5s.png)

![截屏2025-10-19 18.50.13](https://img.tony102.com/i/2025/10/19/uljn1a.png)

#### 类型2: 后缀（子串）匹配型

说白了，就是 KMP。想一下，KMP 做的事情是匹配一个真前缀和真后缀是吧。那么假设我们已经有了一个匹配所有合法串的自动机，那么现在这个自动机要判定一个新的串是否合法，可以把 initial state 当作构造串的分隔符（也就是吧新输入的串当作后缀，自动机里的串当作前缀）。那么这个自动机的状态就是要设计成匹配所有长度的后缀的状态。

感觉说的比较抽象。下面来点例子：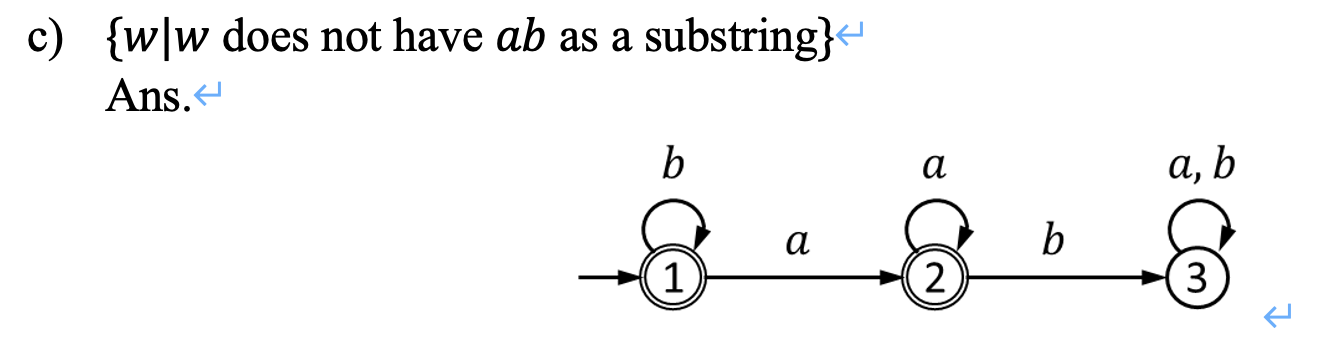

![截屏2025-10-19 19.00.23](https://img.tony102.com/i/2025/10/19/vfe2vj.png)

#### 类型3: 匹配带条件后缀（子串）型

一个例子：

> {w|w contains no runs of length less than four}. A run in a string is a substring of length at least one and consisting entirely of the same symbol. For example, abbbaab has four runs: a, bbb, aa, b.

做这个不要慌，先化简一下问题。假如我们现在要搞一个DFA来匹配不包含长度 $\leq 4$ 的全由 $a$ 组成的子串的串。那么很显然构造的DFA至少要有四条 $a$ 的转移边：

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="400" height="160" version="1.1" xmlns="http://www.w3.org/2000/svg">
    <g transform="scale(0.6)">
        <ellipse stroke="black" stroke-width="1" fill="none" cx="85.5" cy="220.5" rx="30" ry="30"/>
        <ellipse stroke="black" stroke-width="1" fill="none" cx="199.5" cy="220.5" rx="30" ry="30"/>
        <ellipse stroke="black" stroke-width="1" fill="none" cx="309.5" cy="220.5" rx="30" ry="30"/>
        <ellipse stroke="black" stroke-width="1" fill="none" cx="419.5" cy="220.5" rx="30" ry="30"/>
        <ellipse stroke="black" stroke-width="1" fill="none" cx="527.5" cy="220.5" rx="30" ry="30"/>
        <polygon stroke="black" stroke-width="1" points="115.5,220.5 169.5,220.5"/>
        <polygon fill="black" stroke-width="1" points="169.5,220.5 161.5,215.5 161.5,225.5"/>
        <text x="137.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
        <polygon stroke="black" stroke-width="1" points="229.5,220.5 279.5,220.5"/>
        <polygon fill="black" stroke-width="1" points="279.5,220.5 271.5,215.5 271.5,225.5"/>
        <text x="249.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
        <polygon stroke="black" stroke-width="1" points="339.5,220.5 389.5,220.5"/>
        <polygon fill="black" stroke-width="1" points="389.5,220.5 381.5,215.5 381.5,225.5"/>
        <text x="359.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
        <polygon stroke="black" stroke-width="1" points="449.5,220.5 497.5,220.5"/>
        <polygon fill="black" stroke-width="1" points="497.5,220.5 489.5,215.5 489.5,225.5"/>
        <text x="468.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
    </g>
</svg>

然后你只要没有走完这四条边的 input 都是非法的，也就是出现 $b$ 就得到 dead state，遂：

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

然后考虑怎么设置 Final state。首先要注意，实际上我们的条件是两个条件的联立：

1. 长度 $\geq 4$
2. 不能存在长度 $< 4$ 的substring

因此：

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

因此，那么这个题只要对称地画出另外一半即可。

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="900" height="600" version="1.1" xmlns="http://www.w3.org/2000/svg">
	<ellipse stroke="black" stroke-width="1" fill="none" cx="436.5" cy="109.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="32.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="165.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="289.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="396.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="396.5" cy="220.5" rx="24" ry="24"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="436.5" cy="400.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="806.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="684.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="580.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="481.5" cy="220.5" rx="30" ry="30"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="481.5" cy="220.5" rx="24" ry="24"/>
	<polygon stroke="black" stroke-width="1" points="407.572,117.448 61.428,212.552"/>
	<polygon fill="black" stroke-width="1" points="61.428,212.552 70.467,215.254 67.817,205.611"/>
	<text x="221.5" y="155.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="62.5,220.5 135.5,220.5"/>
	<polygon fill="black" stroke-width="1" points="135.5,220.5 127.5,215.5 127.5,225.5"/>
	<text x="93.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="195.5,220.5 259.5,220.5"/>
	<polygon fill="black" stroke-width="1" points="259.5,220.5 251.5,215.5 251.5,225.5"/>
	<text x="222.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="319.5,220.5 366.5,220.5"/>
	<polygon fill="black" stroke-width="1" points="366.5,220.5 358.5,215.5 358.5,225.5"/>
	<text x="337.5" y="241.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="59.903,232.709 409.097,388.291"/>
	<polygon fill="black" stroke-width="1" points="409.097,388.291 403.824,380.468 399.754,389.602"/>
	<text x="219.5" y="331.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon stroke="black" stroke-width="1" points="190.49,237.098 411.51,383.902"/>
	<polygon fill="black" stroke-width="1" points="411.51,383.902 407.613,375.31 402.08,383.64"/>
	<text x="285.5" y="331.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon stroke="black" stroke-width="1" points="308.476,243.736 417.524,377.264"/>
	<polygon fill="black" stroke-width="1" points="417.524,377.264 416.336,367.905 408.591,374.23"/>
	<text x="347.5" y="330.5" font-family="Times New Roman" font-size="20">b</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 449.725,427.297 A 22.5,22.5 0 1 1 423.275,427.297"/>
	<text x="424.5" y="489.5" font-family="Times New Roman" font-size="20">a,b</text>
	<polygon fill="black" stroke-width="1" points="423.275,427.297 414.527,430.83 422.618,436.708"/>
	<path stroke="black" stroke-width="1" fill="none" d="M 414.904,244.043 A 22.5,22.5 0 1 1 389.007,249.428"/>
	<text x="411.5" y="308.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon fill="black" stroke-width="1" points="389.007,249.428 381.162,254.668 390.28,258.776"/>
	<polygon stroke="black" stroke-width="1" points="406.671,192.277 426.329,137.723"/>
	<polygon fill="black" stroke-width="1" points="426.329,137.723 418.913,143.555 428.321,146.945"/>
	<text x="398.5" y="163.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon stroke="black" stroke-width="1" points="465.235,118.12 777.765,211.88"/>
	<polygon fill="black" stroke-width="1" points="777.765,211.88 771.539,204.792 768.666,214.37"/>
	<text x="624.5" y="155.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon stroke="black" stroke-width="1" points="776.5,220.5 714.5,220.5"/>
	<polygon fill="black" stroke-width="1" points="714.5,220.5 722.5,225.5 722.5,215.5"/>
	<text x="740.5" y="241.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon stroke="black" stroke-width="1" points="654.5,220.5 610.5,220.5"/>
	<polygon fill="black" stroke-width="1" points="610.5,220.5 618.5,225.5 618.5,215.5"/>
	<text x="627.5" y="241.5" font-family="Times New Roman" font-size="20">b</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 487.071,249.859 A 22.5,22.5 0 1 1 461.586,242.78"/>
	<text x="450.5" y="307.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon fill="black" stroke-width="1" points="461.586,242.78 452.212,243.843 458.434,251.672"/>
	<polygon stroke="black" stroke-width="1" points="550.5,220.5 511.5,220.5"/>
	<polygon fill="black" stroke-width="1" points="511.5,220.5 519.5,225.5 519.5,215.5"/>
	<text x="525.5" y="241.5" font-family="Times New Roman" font-size="20">b</text>
	<polygon stroke="black" stroke-width="1" points="470.229,192.698 447.771,137.302"/>
	<polygon fill="black" stroke-width="1" points="447.771,137.302 446.143,146.595 455.41,142.838"/>
	<text x="466.5" y="162.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="660.221,238.122 460.779,382.878"/>
	<polygon fill="black" stroke-width="1" points="460.779,382.878 470.19,382.225 464.316,374.132"/>
	<text x="565.5" y="331.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="779.523,233.624 463.477,387.376"/>
	<polygon fill="black" stroke-width="1" points="463.477,387.376 472.858,388.372 468.484,379.38"/>
	<text x="626.5" y="331.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon stroke="black" stroke-width="1" points="561.759,243.926 455.241,377.074"/>
	<polygon fill="black" stroke-width="1" points="455.241,377.074 464.143,373.95 456.334,367.704"/>
	<text x="514.5" y="330.5" font-family="Times New Roman" font-size="20">a</text>
</svg>

#### 设计 NFA

说实话，设计 NFA 应该是一个不会考的题型。因为合法的NFA应该是不唯一的。只要注意 NFA 的 transition function 是 partial function，然后也不需要考虑所谓的 input 顺序，因为，input string 只要在 NFA 找到一条路径到 final states 就行。简单给一个例子吧：

设计一个 NFA 接受：The language $1^{*}(001^+)^*$ with three states

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

#### Union and Concatenation of NFA

比较好说：

- Concatenation 就是把 M1 和 M2 用一个 $\epsilon$ transition 连起来即可
- Union 就是把 M1 和 M2 的 initial states，用 $\epsilon$ transition 连到一个新的 state 即可。

### 做题2: NFA2DFA

**一句话：找闭包然后连接**

1. 首先你要找到 Initial state 的 $\epsilon-$closure，然后这些状态都是要加入DFA的initial state作为新的 DFA 的initial state的
2. 然后枚举每一条出边，先记下来到达的集合，再计算到达集合的 $\epsilon-$closure。**检查这个状态是否已经存在，如果不存在就建立一个新状态然后连接，否则直接连接。**

**例外：加入 NFA 没有某一个符号的出边，那么在新的 DFA 中要建立一个 dead state 然后死循环**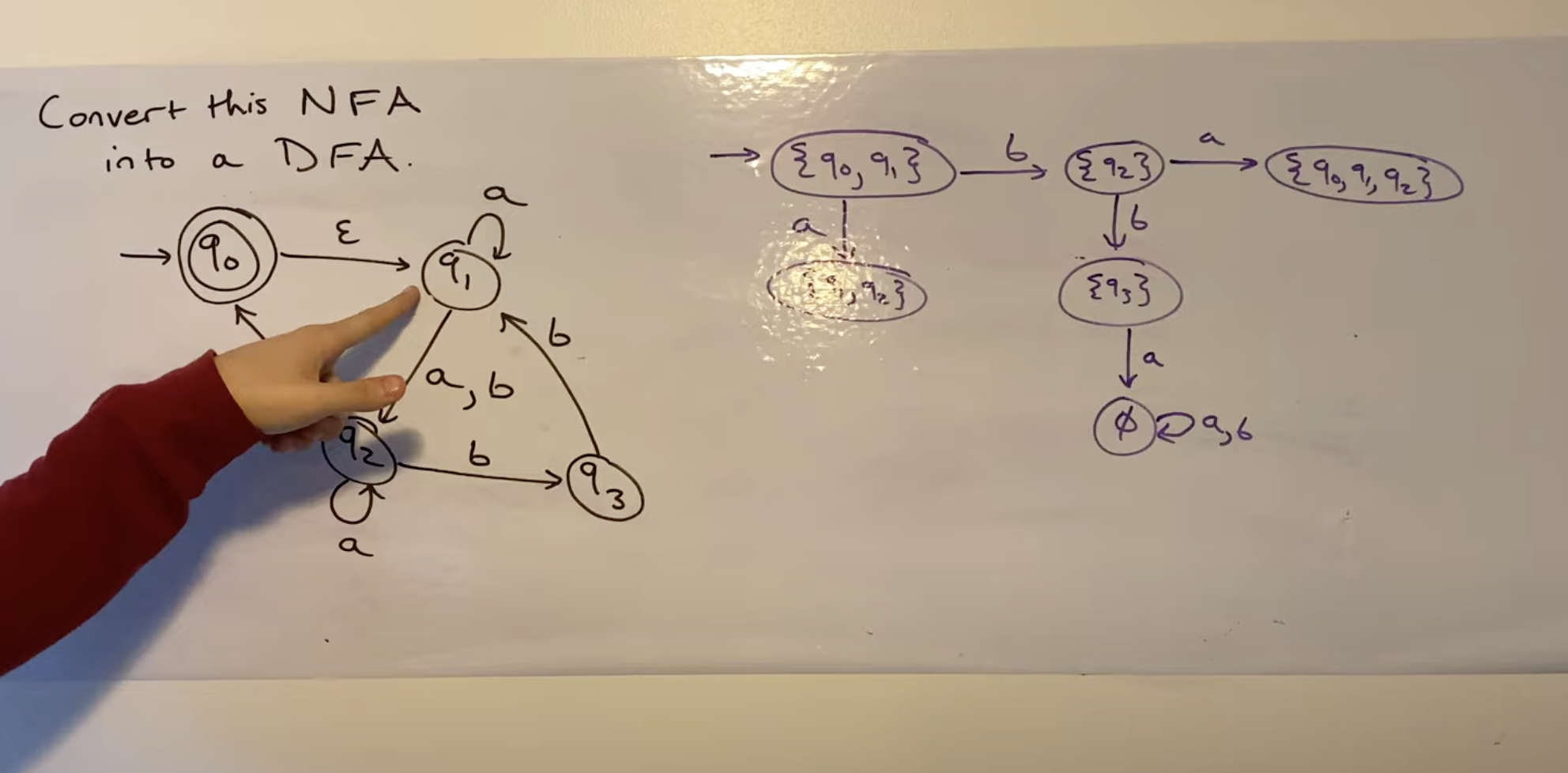

![image](https://img.tony102.com/i/2025/10/19/uitfk6.png)

比如说图中的 $\{q_3\}$ 由于没有 $a$ 的出边，在新的 DFA 中就要连接一个 dead state 并且设置死循环

### 做题3：多个 DFA 的叉积

本质上，多个 DFA 的叉积等价于对 state sets 做叉积 + 对 transition function 做叉积。在此给出一个比较方便做题的方法：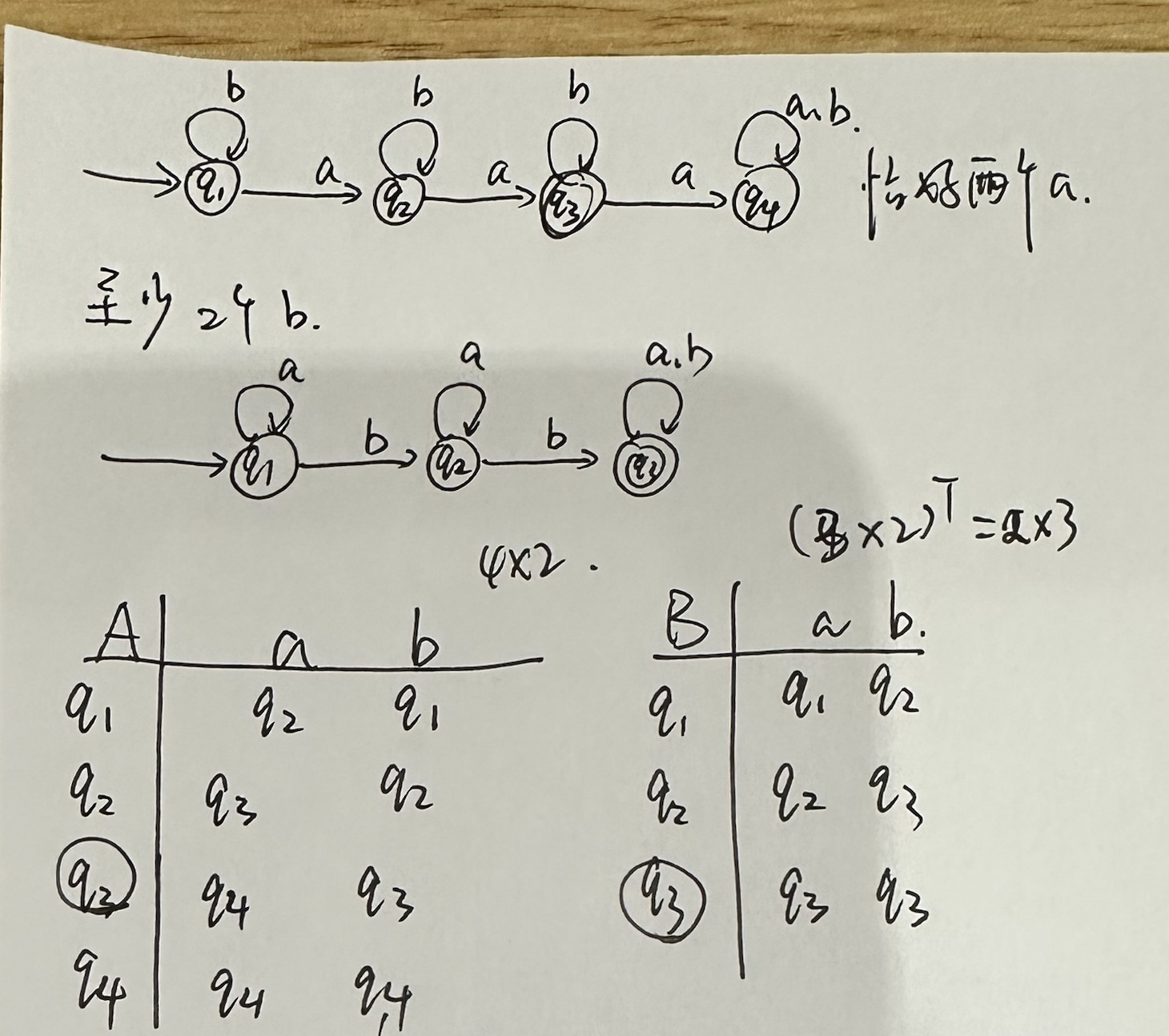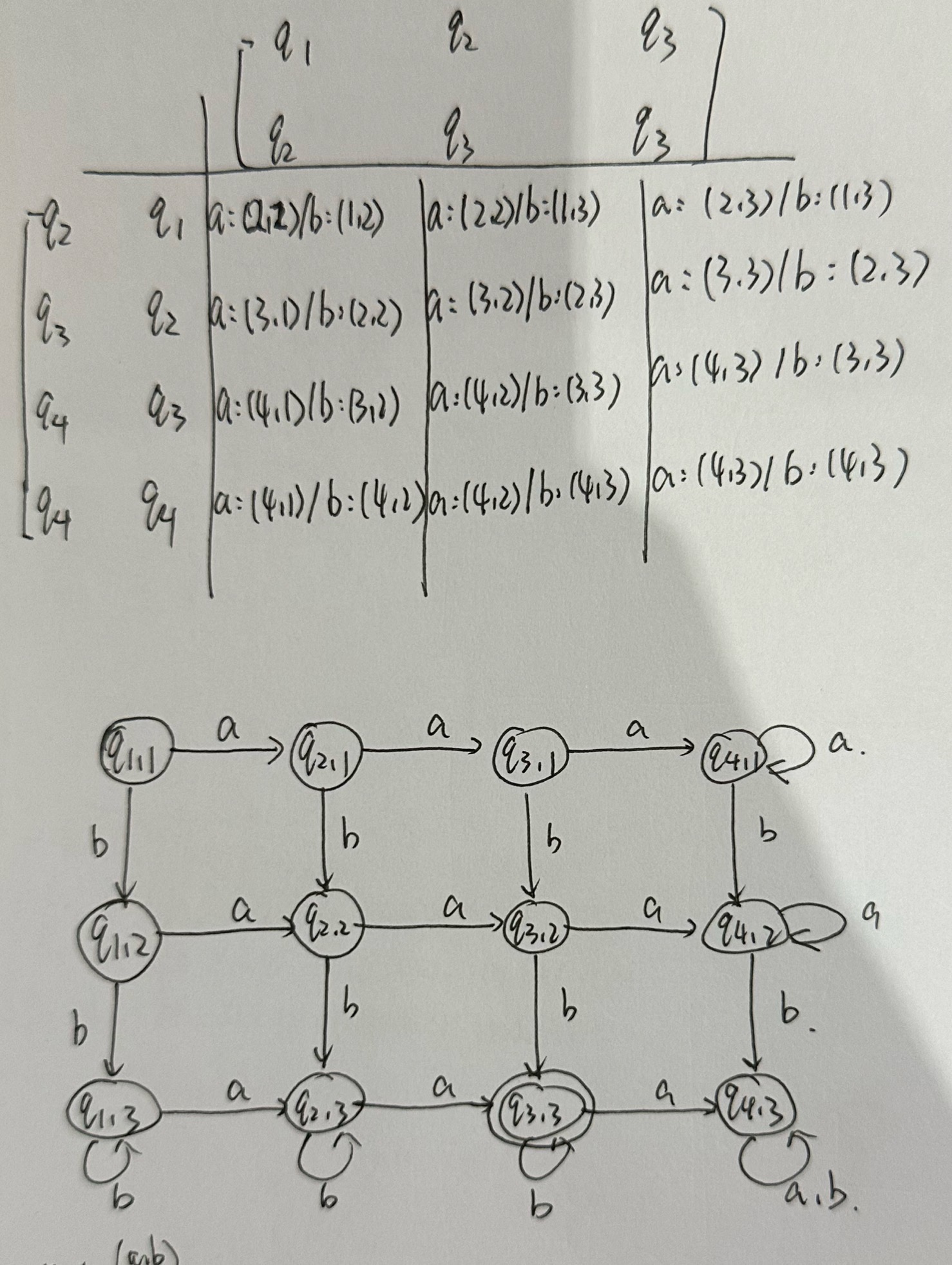

![c0971633a514310628eb5ad2c5a31d1e](https://img.tony102.com/i/2025/11/08/n7bb07.jpg)
![b040dcd3b8a3fd2a1d04c63a324112fc](https://img.tony102.com/i/2025/11/08/n7dxwc.jpg)

## Lec05: Regular Language

To study the properties of regular languages, we define the regular operations.

### Definition

Let $ A $ and $ B $ be languages.

- **Union**: $ A \cup B = \{ x \mid x \in A \text{ or } x \in B \} $
- **Concatenation**: $ A \circ B = \{ xy \mid x \in A \text{ and } y \in B \} $
- **Star**: $ A^* = \{ x_1 x_2 \cdots x_k \mid k \geq 0 \text{ and each } x_i \in A \} $

Note: each $ x_i $ is a string in the language $ A $. And $ x_1 x_2 \cdots x_k $ is the concatenation of $ x_1, x_2, $ until $ x_k $. Equivalently, $ A^* = A^0 \cup A^1 \cup A^2 \cup \cdots $

### Regular Expression

当时上课的时候没怎么认真听，觉得是个简单内容。后来发现这个东西会在 CFG 中间出现。遂导致掉线。不过本来CFG那节课我也没去，忘了是什么原因了。

- 正则语言可以递归构造。
- 正则表达式描述了正则语言中字符串的 common 模式（与机器无关）。

#### 定义（递归定义）

如果 $ R $ 满足以下条件，则 $ R $ 是字母表 $ \Sigma $ 上的正则表达式：

- **基础情况**
  - $ a $，其中 $ a \in \Sigma $，
  - $ \varepsilon $，或
  - $ \emptyset $
- **递归情况**
  - $ (R_1 \cup R_2) $，其中 $ R_1 $ 和 $ R_2 $ 是正则表达式，
  - $ (R_1 \circ R_2) $，其中 $ R_1 $ 和 $ R_2 $ 是正则表达式，或
  - $ (R_1^*) $，其中 $ R_1 $ 是正则表达式。

### Languages Defined by Regular Expression

一种 language 的 regular expression 展示了该 language 中所有string的共同模式。因此，

#### 定义

设 $ R $ 是一个正则表达式。由 $ R $ 定义的语言 $ L(R) $ 为：

- **基础情况**：
  - $ L(\emptyset) = \emptyset $
  - $ L(\varepsilon) = \{ \varepsilon \} $
  - $ \forall a \in \Sigma $，$ L(a) = \{ a \} $
- **递归情况**：
  - 如果 $ R = R_1 \cup R_2 $，那么 $ L(R_1 \cup R_2) = L(R_1) \cup L(R_2) $
  - 如果 $ R = R_1 \circ R_2 $，那么 $ L(R_1 \circ R_2) = L(R_1) \circ L(R_2) $
  - 如果 $ R = R_1^* $，那么 $ L(R_1^*) = (L(R_1))^* $

### 做题4: 证明 Languages 的等价性（or 不等价）

挖坑待填，其实是不会

### 做题6: NFA2Regular Expression

说白了，课件给的代码就是Floyd。相当于你的转移有两种：

1. $i \to k \to j$
2. $k \to k$ 走自环

所以，要消除 $k$ 这个中间点，连成 $i \to k* \to j$ 即可。

实操一个比较好的办法是弄一个“超级源点”和“超级汇点” （当然不是网络流），然后每次记录 in 和 out （相当于枚举 $k$）。见 assignment 1 Q5。这里给出两个更难一点的例子

#### Example 1

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<svg width="800" height="600" version="1.1" xmlns="http://www.w3.org/2000/svg">
	<ellipse stroke="black" stroke-width="1" fill="none" cx="105.5" cy="100.5" rx="30" ry="30"/>
	<text x="100.5" y="106.5" font-family="Times New Roman" font-size="20">1</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="268.5" cy="100.5" rx="30" ry="30"/>
	<text x="263.5" y="106.5" font-family="Times New Roman" font-size="20">2</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="268.5" cy="100.5" rx="24" ry="24"/>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="95.5" cy="184.5" rx="30" ry="30"/>
	<text x="91.5" y="190.5" font-family="Times New Roman" font-size="20">s</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="95.5" cy="281.5" rx="30" ry="30"/>
	<text x="90.5" y="287.5" font-family="Times New Roman" font-size="20">1</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="268.5" cy="281.5" rx="30" ry="30"/>
	<text x="263.5" y="287.5" font-family="Times New Roman" font-size="20">2</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="268.5" cy="184.5" rx="30" ry="30"/>
	<text x="265.5" y="190.5" font-family="Times New Roman" font-size="20">t</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="96.5" cy="366.5" rx="30" ry="30"/>
	<text x="92.5" y="372.5" font-family="Times New Roman" font-size="20">s</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="96.5" cy="472.5" rx="30" ry="30"/>
	<text x="91.5" y="478.5" font-family="Times New Roman" font-size="20">1</text>
	<ellipse stroke="black" stroke-width="1" fill="none" cx="290.5" cy="472.5" rx="30" ry="30"/>
	<text x="287.5" y="478.5" font-family="Times New Roman" font-size="20">t</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 134.486,92.829 A 262.336,262.336 0 0 1 239.514,92.829"/>
	<polygon fill="black" stroke-width="1" points="239.514,92.829 232.677,86.329 230.675,96.126"/>
	<text x="181.5" y="78.5" font-family="Times New Roman" font-size="20">b</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 240.031,109.884 A 215.402,215.402 0 0 1 133.969,109.884"/>
	<polygon fill="black" stroke-width="1" points="133.969,109.884 140.492,116.699 142.954,107.007"/>
	<text x="181.5" y="137.5" font-family="Times New Roman" font-size="20">b</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 295.297,87.275 A 22.5,22.5 0 1 1 295.297,113.725"/>
	<text x="341.5" y="106.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon fill="black" stroke-width="1" points="295.297,113.725 298.83,122.473 304.708,114.382"/>
	<path stroke="black" stroke-width="1" fill="none" d="M 78.703,113.725 A 22.5,22.5 0 1 1 78.703,87.275"/>
	<text x="22.5" y="106.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon fill="black" stroke-width="1" points="78.703,87.275 75.17,78.527 69.292,86.618"/>
	<polygon stroke="black" stroke-width="1" points="105.5,23.5 105.5,70.5"/>
	<polygon fill="black" stroke-width="1" points="105.5,70.5 110.5,62.5 100.5,62.5"/>
	<path stroke="black" stroke-width="1" fill="none" d="M 68.703,294.725 A 22.5,22.5 0 1 1 68.703,268.275"/>
	<text x="12.5" y="287.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon fill="black" stroke-width="1" points="68.703,268.275 65.17,259.527 59.292,267.618"/>
	<polygon stroke="black" stroke-width="1" points="95.5,214.5 95.5,251.5"/>
	<polygon fill="black" stroke-width="1" points="95.5,251.5 100.5,243.5 90.5,243.5"/>
	<path stroke="black" stroke-width="1" fill="none" d="M 124.227,272.914 A 252.35,252.35 0 0 1 239.773,272.914"/>
	<polygon fill="black" stroke-width="1" points="239.773,272.914 233.13,266.215 230.841,275.95"/>
	<text x="176.5" y="257.5" font-family="Times New Roman" font-size="20">b</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 239.292,288.299 A 317.485,317.485 0 0 1 124.708,288.299"/>
	<polygon fill="black" stroke-width="1" points="124.708,288.299 131.674,294.66 133.479,284.824"/>
	<text x="176.5" y="314.5" font-family="Times New Roman" font-size="20">b</text>
	<path stroke="black" stroke-width="1" fill="none" d="M 295.297,268.275 A 22.5,22.5 0 1 1 295.297,294.725"/>
	<text x="341.5" y="287.5" font-family="Times New Roman" font-size="20">a</text>
	<polygon fill="black" stroke-width="1" points="295.297,294.725 298.83,303.473 304.708,295.382"/>
	<polygon stroke="black" stroke-width="1" points="268.5,251.5 268.5,214.5"/>
	<polygon fill="black" stroke-width="1" points="268.5,214.5 263.5,222.5 273.5,222.5"/>
	<path stroke="black" stroke-width="1" fill="none" d="M 109.725,499.297 A 22.5,22.5 0 1 1 83.275,499.297"/>
	<text x="47.5" y="561.5" font-family="Times New Roman" font-size="20">a | ba*b</text>
	<polygon fill="black" stroke-width="1" points="83.275,499.297 74.527,502.83 82.618,508.708"/>
	<polygon stroke="black" stroke-width="1" points="96.5,396.5 96.5,442.5"/>
	<polygon fill="black" stroke-width="1" points="96.5,442.5 101.5,434.5 91.5,434.5"/>
	<polygon stroke="black" stroke-width="1" points="126.5,472.5 260.5,472.5"/>
	<polygon fill="black" stroke-width="1" points="260.5,472.5 252.5,467.5 252.5,477.5"/>
	<text x="178.5" y="493.5" font-family="Times New Roman" font-size="20">ba*</text>
</svg>

比如这里的步骤是消除 2，那么画表（入度和出度）：

| in   | Out  | Edge                     |
| ---- | ---- | ------------------------ |
| 1    | t    | (1 -> t): ba*            |
|      | 1    | (1 -> 1): $a \cup ba^*b$ |

#### Example 2

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

最后的结果显然是一个 union 形式的 NFA

## Lec 06: Pumping Lemma （包含 Context-Free Language 版本）

尝试策清楚，不一定对。不过一定会保证做题是对的。

### 正确性证明

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

抄一下定义：

If $A$ is a regular language, then there is a positive constant $p$ such that every string $w \in A$ of length at least $p$ can be written as $w = xyz$ satisfying the following conditions:

- $\forall i \geq 0, xy^iz \in A$
- $|y| > 0$ and 
- $|xy| \leq p$

其中 $p$ 是 pumping length

想一下为什么是对的。

1. 首先 regular language 一定是一个可以被 DFA 或者 NFA 识别的 language。所以我们对于这个 $A$ 是一定可以构造一个 DFA/NFA 来识别的。为了方便，以下讨论 DFA。
2. 假设 $n$ 是这个 DFA 的 state 的数量
3. 假设 $w \in L$ 并且 $|w| \geq n$
4. **在这个自动机读入 $w$ 的前 $n$ 个字符后一定有一个状态达到过两次**

感觉这里是要详细说明一下的，如果不搞懂的话后面非常不好懂。$|w| = 0$ 的情形先不讨论了，直接看 $|w| \geq 1$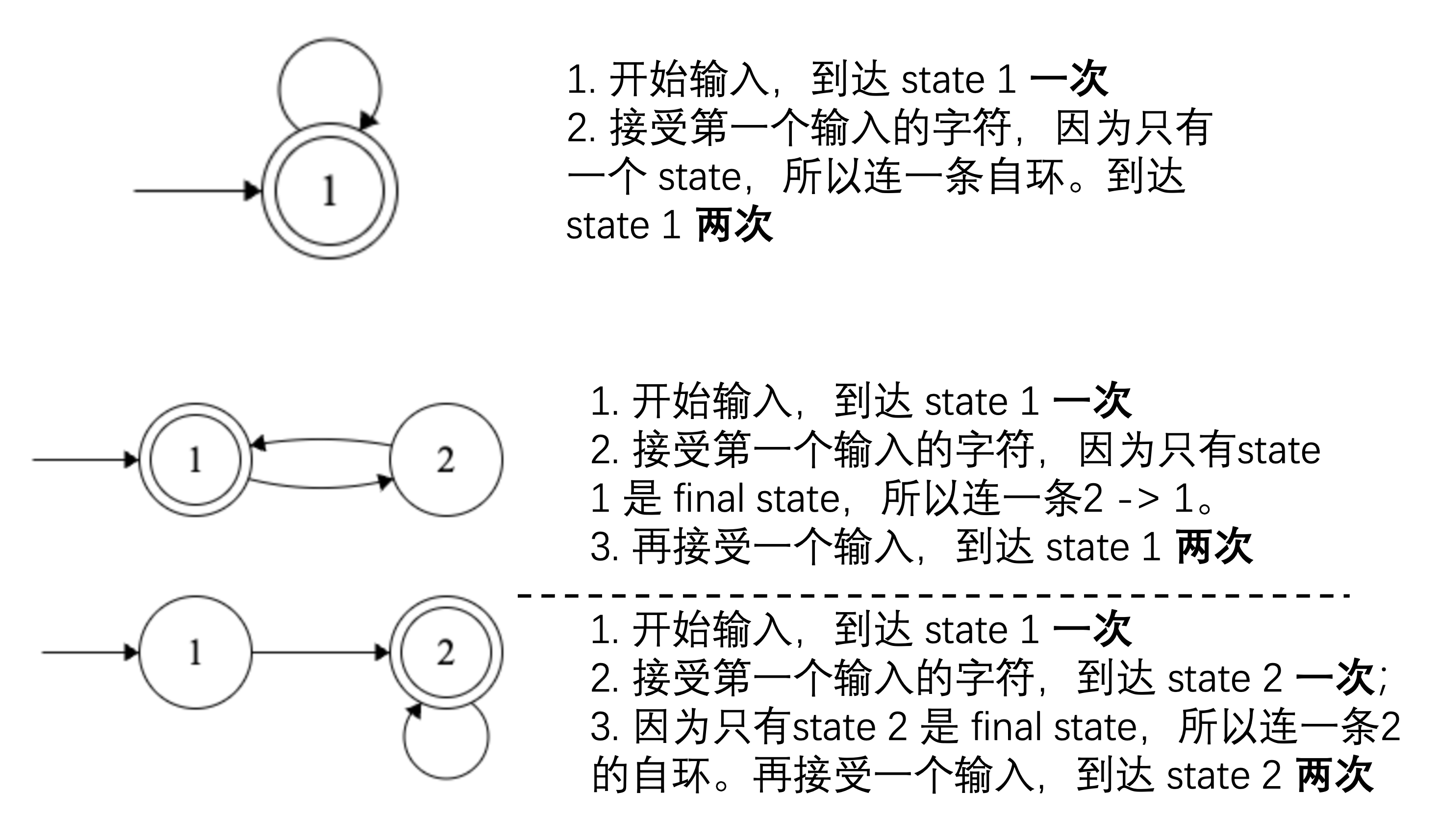

![图片 1](https://img.tony102.com/i/2025/11/08/mg3o6z.png)

5. 所以就是说，必然存在一个 state 被重复走了。对应上面的 $y$

### 做题 5: 证明一个 Language 不是 regular language

**反证法证明** ：套路大概如下：

1. 假设要证明的 language 是 regular language
2. $n$ 是未知的 
3. $w$ 可以在满足 $w \in L$ 和 $|w| \geq n$ 的条件下自由选择
4. $x, y, z$ 也是未知的
5. 找到一个 $k$ 使得 $xy^kz \not\in L$

还是非常抽象，来看一些例子。**见另外一个文档。**

### 证明 Language type 方法的总结

给定一个 language $L$

- To prove $L$ is regular 
  -  construct a DFA/NFA
- To prove $L$ is not regular
  - Use pumping lemma (For Reg)
- To prove $L$ is CFG
  - construct PDA
- To prove $L$ is not CFG
  - Pumping lemma (For CF)
    - Lec 8: P? $L = \{a^nb^nc^n| n \geq 0\}$ is not CF

## Lec 02: Math

好像是一些概念，先放点重要的

### Constructive Proof

**规范步骤：**

1. Used to prove a predicate with existential quantifiers, *i.e.* $\exist x, P(x)$
2. First, construct an object $x$
3. Second, prove $P(x)$ is true

## Contradiction Proof

懒得写了，大概就是：

1. 写一个命题 $\exist x, P(x)$
2. 然后给出逆否命题 $\exist \neg x$，并且证明 $P(\neg x)$ 为真
3. 自然得到 $x$ 为假

### Induction

要证明 $\forall x \in \mathbb{N}, P(x)$，一句话：**一般归纳法只要 $k \to k+1$ 就行，但是 strong induction 要求** $1 \land 2 \land 3 \land \dots \land k \to k + 1$

### Cardinality （范数）

首先抄一下定义：

![Cardinality](https://img.tony102.com/i/2025/10/19/sdo8h0.png)

![截屏2025-10-19 17.16.30](https://img.tony102.com/i/2025/10/19/sdvhz8.png)

证明 **Countable/Uncountable** 的方法主要有两个方法

## Lec 03/04: (Non-)Finite Automata

定义：需要包含一下元素

5 tuple $(Q, \Sigma, \delta, q_0, F)$ where:

### 做题1：设计 DFA / NFA

#### 类型1: 数量型

这类是比较简单的题型。**Solution: 设计足够的转移边来满足数量匹配即可。**

比如说：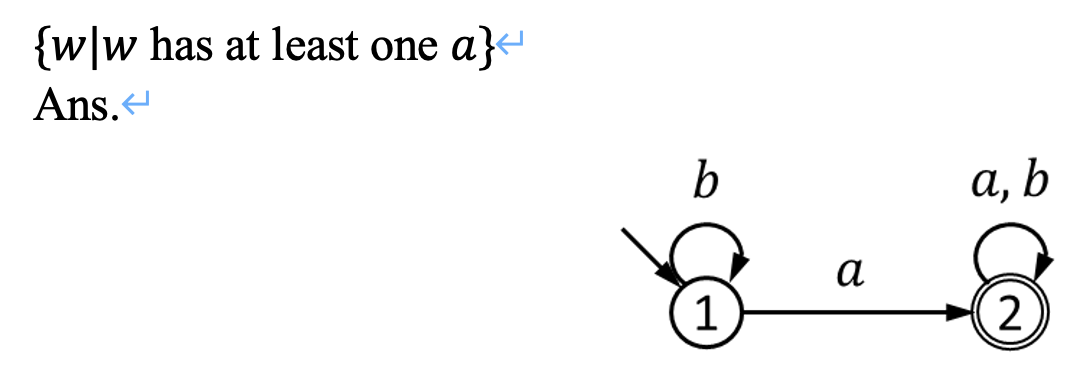

![image](https://img.tony102.com/i/2025/10/19/ul2x5s.png)

![截屏2025-10-19 18.50.13](https://img.tony102.com/i/2025/10/19/uljn1a.png)

#### 类型2: 后缀（子串）匹配型

感觉说的比较抽象。下面来点例子：

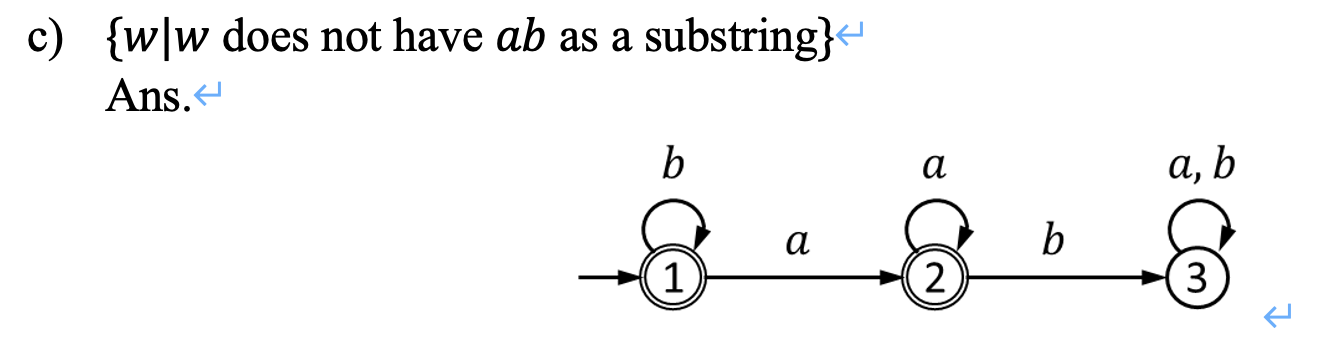![截屏2025-10-19 19.00.23](https://img.tony102.com/i/2025/10/19/vfe2vj.png)

#### 类型3: 匹配带条件后缀（子串）型

一个例子：

<?xml version="1.0" standalone="no"?>

然后你只要没有走完这四条边的 input 都是非法的，也就是出现 $b$ 就得到 dead state，遂：

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

然后考虑怎么设置 Final state。首先要注意，实际上我们的条件是两个条件的联立：

1. 长度 $\geq 4$
2. 不能存在长度 $< 4$ 的substring

因此：

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

因此，那么这个题只要对称地画出另外一半即可。

<?xml version="1.0" standalone="no"?>

#### 设计 NFA

设计一个 NFA 接受：The language $1^{*}(001^+)^*$ with three states

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

#### Union and Concatenation of NFA

比较好说：

- Concatenation 就是把 M1 和 M2 用一个 $\epsilon$ transition 连起来即可
- Union 就是把 M1 和 M2 的 initial states，用 $\epsilon$ transition 连到一个新的 state 即可。

### 做题2: NFA2DFA

**一句话：找闭包然后连接**

**例外：加入 NFA 没有某一个符号的出边，那么在新的 DFA 中要建立一个 dead state 然后死循环**

![image](https://img.tony102.com/i/2025/10/19/uitfk6.png)

比如说图中的 $\{q_3\}$ 由于没有 $a$ 的出边，在新的 DFA 中就要连接一个 dead state 并且设置死循环

### 做题3：多个 DFA 的叉积

本质上，多个 DFA 的叉积等价于对 state sets 做叉积 + 对 transition function 做叉积。在此给出一个比较方便做题的方法：

![c0971633a514310628eb5ad2c5a31d1e](https://img.tony102.com/i/2025/11/08/n7bb07.jpg)
![b040dcd3b8a3fd2a1d04c63a324112fc](https://img.tony102.com/i/2025/11/08/n7dxwc.jpg)

## Lec05: Regular Language

To study the properties of regular languages, we define the regular operations.

### Definition

Let $ A $ and $ B $ be languages.

Note: each $ x_i $ is a string in the language $ A $. And $ x_1 x_2 \cdots x_k $ is the concatenation of $ x_1, x_2, $ until $ x_k $. Equivalently, $ A^* = A^0 \cup A^1 \cup A^2 \cup \cdots $

### Regular Expression

- 正则语言可以递归构造。
- 正则表达式描述了正则语言中字符串的 common 模式（与机器无关）。

#### 定义（递归定义）

如果 $ R $ 满足以下条件，则 $ R $ 是字母表 $ \Sigma $ 上的正则表达式：

### Languages Defined by Regular Expression

一种 language 的 regular expression 展示了该 language 中所有string的共同模式。因此，

#### 定义

设 $ R $ 是一个正则表达式。由 $ R $ 定义的语言 $ L(R) $ 为：

### 做题4: 证明 Languages 的等价性（or 不等价）

挖坑待填，其实是不会

### 做题6: NFA2Regular Expression

说白了，课件给的代码就是Floyd。相当于你的转移有两种：

1. $i \to k \to j$
2. $k \to k$ 走自环

所以，要消除 $k$ 这个中间点，连成 $i \to k* \to j$ 即可。

#### Example 1

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">
<?xml version="1.0" standalone="no"?>

比如这里的步骤是消除 2，那么画表（入度和出度）：

| in   | Out  | Edge                     |
| ---- | ---- | ------------------------ |
| 1    | t    | (1 -> t): ba*            |
|      | 1    | (1 -> 1): $a \cup ba^*b$ |

#### Example 2

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

最后的结果显然是一个 union 形式的 NFA

## Lec 06: Pumping Lemma （包含 Context-Free Language 版本）

尝试策清楚，不一定对。不过一定会保证做题是对的。

### 正确性证明

<?xml version="1.0" standalone="no"?>

<!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "https://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd">

抄一下定义：

If $A$ is a regular language, then there is a positive constant $p$ such that every string $w \in A$ of length at least $p$ can be written as $w = xyz$ satisfying the following conditions:

- $\forall i \geq 0, xy^iz \in A$
- $|y| > 0$ and 
- $|xy| \leq p$

其中 $p$ 是 pumping length

想一下为什么是对的。

感觉这里是要详细说明一下的，如果不搞懂的话后面非常不好懂。$|w| = 0$ 的情形先不讨论了，直接看 $|w| \geq 1$

![图片 1](https://img.tony102.com/i/2025/11/08/mg3o6z.png)

5. 所以就是说，必然存在一个 state 被重复走了。对应上面的 $y$

### 做题 5: 证明一个 Language 不是 regular language

**反证法证明** ：套路大概如下：

还是非常抽象，来看一些例子。**见另外一个文档。**

### 证明 Language type 方法的总结

给定一个 language $L$

最后修改：2025 年 11 月 09 日

如果觉得我的文章对你有用，请随意赞赏

1 条评论

鍗庣撼鍏徃鍚堜綔寮€鎴锋墍闇€鏉愭枡锛熺數璇濆彿鐮?5587291507 寰俊STS5099
November 9th, 2025 at 02:40 am

果博东方客服开户联系方式【182-8836-2750—】?薇- cxs20250806】
果博东方公司客服电话联系方式【182-8836-2750—】?薇- cxs20250806】
果博东方开户流程【182-8836-2750—】?薇- cxs20250806】
果博东方客服怎么联系【182-8836-2750—】?薇- cxs20250806】

回复