BZOJ4237 稻草人

tony102

2021 年 06 月 18 日

1154 次浏览

暂无评论

1821字数

题解

[Hydro BZOJ](https://hydro.org.cn/d/bzoj/p/P4237)

这是我新发现的一个比 darkBZOJ 不知道快到哪里去的OJ，就是它的题面还要靠人工一点点修正。真是一个伟大的目标

## Sol

有一个月没更博了...

首先暴力的搞法就是枚举每一个左下角，然后暴力看哪一些点可以贡献成为右上角

现在主要的问题在于确定右上角，那么来看看右上角都有哪些特点。

我们先设我们现在处理的左下角 $A$ 点在 $(x_1, y_1)$ 的位置

首先，假如有一列候选的右上角的点，它们的恒左边相同，此时只有最下面的点可以成为右上角。这一点比较显然。

现在考虑其他的点对 $A$ 点的影响，借 yyb 的图用一下

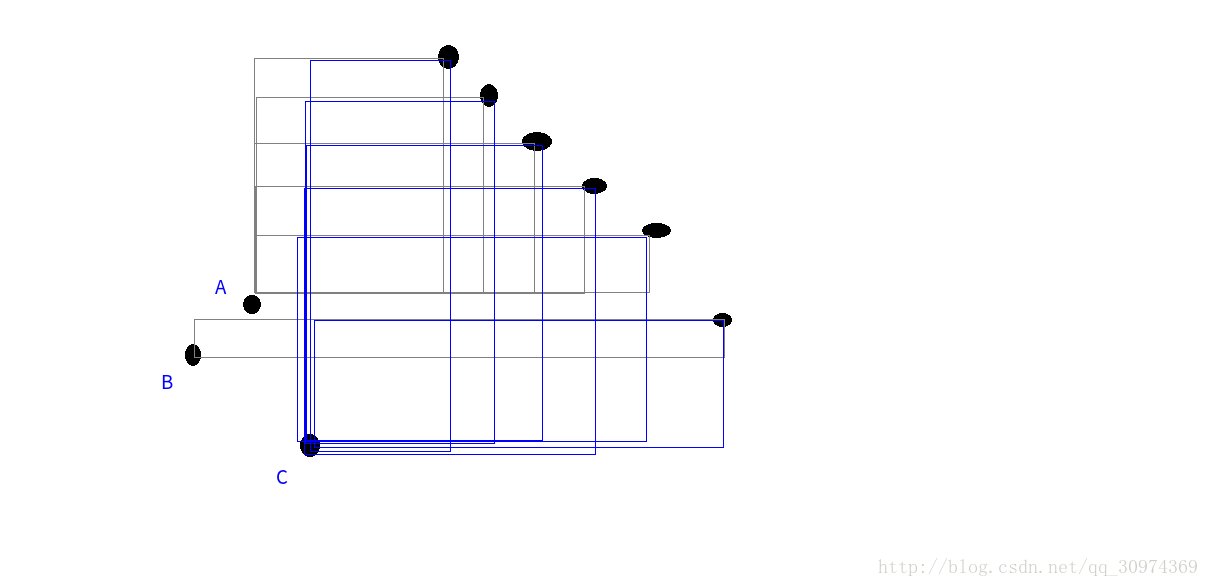![20180205192608935.png](https://z3.ax1x.com/2021/08/20/fX3nAg.png)

此时对于 $C$ 点来说，没有受到 $A$，$B$ 两点的贡献限制。但是很显然 $B$ 受到了 $A$ 的限制。可以看出来，一个点的横坐标如果比另外一个点的要大，它就会影响那些点的贡献。

那么应该用cdq分治搞的想法应该就出来了。首先肯定要对 $x$ 轴坐标排序。然后按照 $y$ 轴坐标从大到小的顺序一次加入处理。对左右两边同时开单调栈，保证 $x$ 轴坐标的单调性。右边的从小到大，左边的从大到小，那么这样就保证了每一个左侧点对在单调栈中前面一个元素影响。也就是说，假如上面那个图不这样做，假如 A B C对于当前的区间都在同一侧， B 可能就会对 A C两个点计算重复的部分。这样用单调栈维护顺序就不会了。

关于每次选入的点，单调栈上二分是常见操作了吧

## Code

```cpp
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int SIZE = 5e5 + 5;

int n; LL ans;
int stal[SIZE], star[SIZE];

struct node {
    int x, y;
    bool operator< (const node &a) const {
        return x < a.x;
    }
} a[SIZE];

namespace GTR {
	const int bufl = 1 << 15;
	char buf[bufl], *s = buf, *t = buf;
	inline int fetch() {
		if (s == t) { t = (s = buf) + fread(buf, 1, bufl, stdin); if (s == t) return EOF; }
		return *s++;
	}
	inline int read() {
		int a = 0, b = 1, c = fetch();
		while (c < 48 || c > 57) b ^= c == '-', c = fetch();
		while (c >= 48 && c <= 57) a = (a << 1) + (a << 3) + c - 48, c = fetch();
		return b ? a : -a;
	}
} using GTR::read;

int cmp(node a, node b) {
    return a.y > b.y;
}

void cdq(int l, int r) {
    if (l == r) return;
    int mid = (l + r) >> 1;
    cdq(l, mid), cdq(mid + 1, r);
    std::sort(a + l, a + mid + 1, cmp); std::sort(a + mid + 1, a + r + 1, cmp);
    int ql = 0, qr = mid + 1, top = 0;
    for (int i = l; i <= mid; ++ i) {
        while (qr <= r && a[qr].y > a[i].y) {
            while (top && a[star[top]].x > a[qr].x) -- top;
            star[++ top] = qr ++;
        }
        while (ql && a[stal[ql]].x < a[i].x) -- ql;
        stal[++ ql] = i;
        if (ql == 1) ans += top;
        else {
            int xl = 1, xr = top, res = top + 1;
            while (xl <= xr) {
                int mi = (xl + xr) >> 1;
                if (a[star[mi]].y > a[stal[ql - 1]].y) xl = mi + 1;
                else res = mi, xr = mi - 1;
            }
            ans += top - res + 1;
        }
    }
}

int main() {
    n = read();
    for (int i = 1; i <= n; ++ i) a[i].x = read(), a[i].y = read();
    std::sort(a + 1, a + n + 1);
    cdq(1, n);
    printf("%lld\n", ans);
    return 0;
}
```

最后修改：2021 年 08 月 20 日