3D Vision: 2D and 1D projective geometry

博主： tony102
发布时间：2024 年 08 月 30 日
246 次浏览
暂无评论
2601字数
分类：总结

## Projective Geometry

### Primary

针对 Projective Geometry 的一些观察：

- 平行线会相交/圆可能会变成椭圆/矩形可能会变成平行四边形
- 但是直线的性质仍然保留

因此，我们可以考虑定义一种 Projective Transformation ，我们仍要保留直线。实际上，我们应该考虑更多这样在几何中具有不变性，并且在设计的 mapping 方式中保留他们。

### Euclidean v.s. Projective

- Euclidean 几何是一种对称几何
- Euclidean 几何利用了 axiomatic method ，例如：compass/straightedge
- Projective Geometry 利用坐标和代数——称为：analytic geometry
- Projective Geometry 将提供一种很好的在无限处的几何表示

### Homogeneous Coordinates

- A point in homogeneous coordinates $(kx, ky, k)$ , corresponds to $(\frac{kx}{k}, \frac{ky}{k})=(x,y)$ in **Cartesian coordinates**
- $(kx, ky, k)$ **is equivalent** for all $k$'s
- 联系到无限处的方便表示，只要 $k = 0$，那么会得到 $(\frac{x}{0}, \frac{y}{0})$ ，这正是一个无穷的
- 不失一般地，$\mathbb{R}^{n}$ 欧式空间可以被延伸成一个 $\mathbb{P}^{n}$ 的投影空间为一个 homogeneous vectors

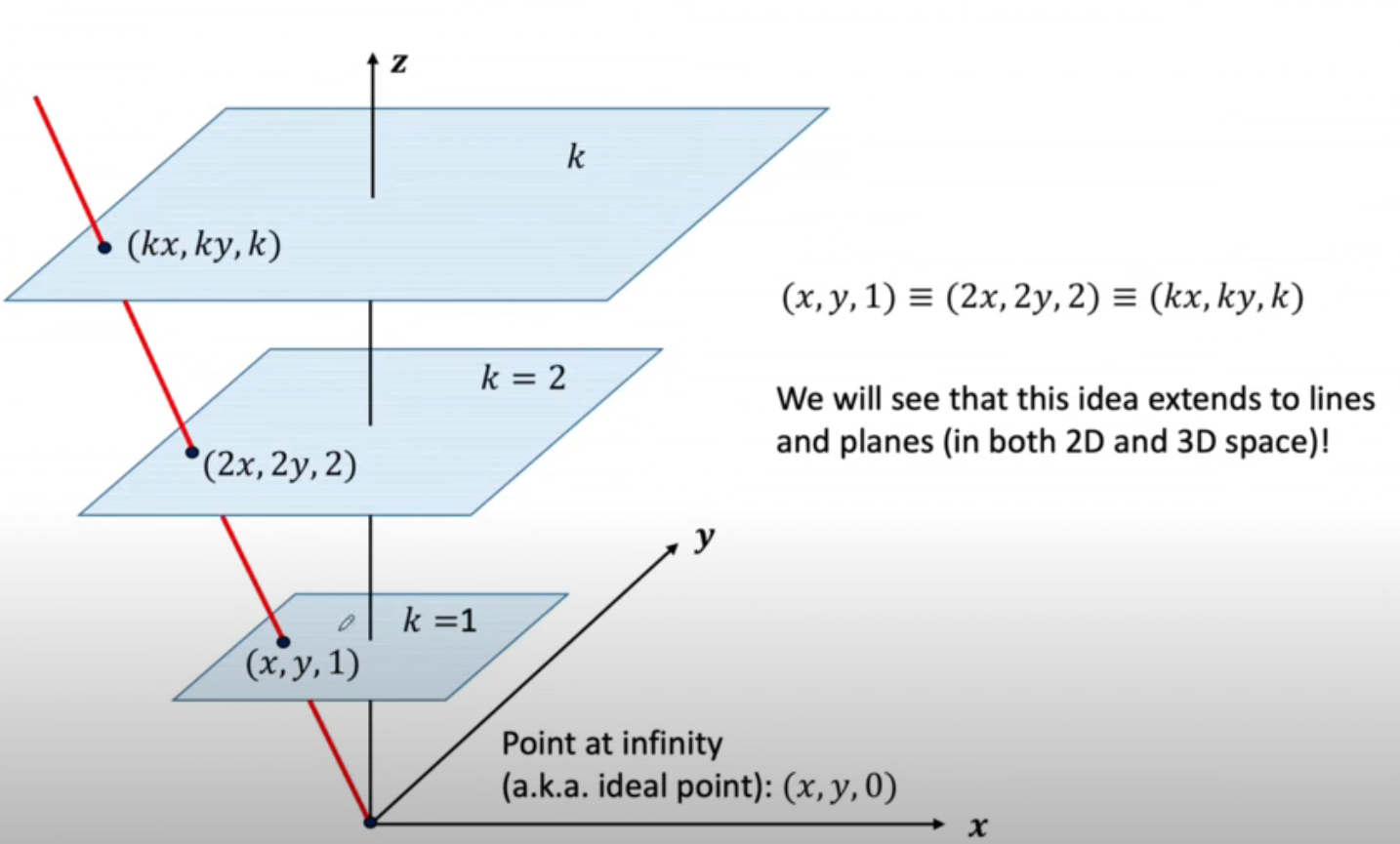![Screenshot 2024-08-30 001923.png](https://s1.locimg.com/2024/08/30/257d8ce11a40b.png)

直观展示。

### The 2D Projective Plane

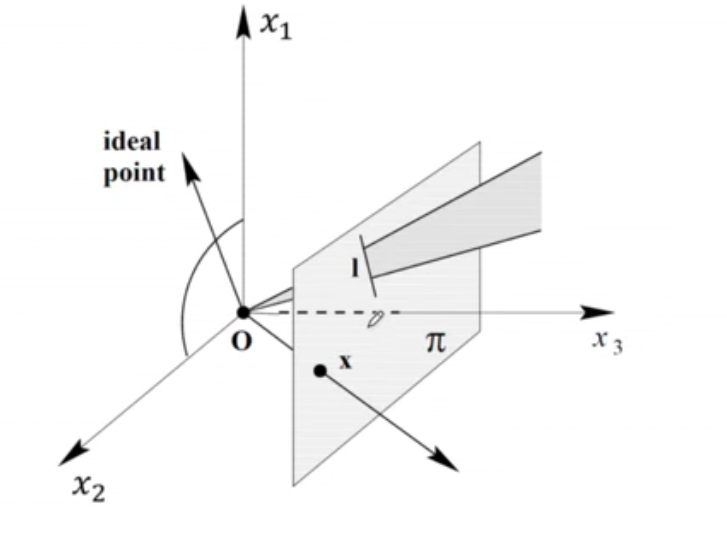![Screenshot 2024-08-30 002229.png](https://s1.locimg.com/2024/08/30/8267707371acc.png)

平面 $\pi$ 可以用其法向量表示（在几何中的标准操作）。在平面中，直线被表示为：$ax+by+c = 0$ ，平面 $\pi$ 上的直线 $l$ 也可以用其法向量 $(a,b,c)^{T}$ 来表示。

### Homogeneous Representation of Lines and Points

我们可以发现，lines 和其 representation (法向量) 并非一一对应。因为，既然 $ax+by+c = 0$ 和 $k(ax+by+c) = 0$ 是一条线，那么 $(a,b,c)^{T}$ 和 $k(a,b,c)^{T}$ 实际上描述的是一条线，对于任何非零的 $k$ （实际上是一个等价类）

**特别地，$(0, 0, 0)^{T}$ 不对应任何直线**

如果一个点 $\vec{x} = (x,y)^{T}$ 在直线 $\vec{l} = (a,b,c)^{T}$ 在直线 $ax+by+c = 0$ 上当且仅当：

$(x, y, 1) (a,b,c)^{T} = 0$

解释：$\vec{l}$ 是直线的法向量，如果点在线上，那么法向量正交 $\vec{l}$  也可以在点 $\vec{x}$ 上。也可以写成 $\vec{x}^{T}\cdot \vec{l} =0$

对非零 $k$ 同样成立。

因此，$(kx,ky,k)^{T} \in \mathbb{P}^{2}$ 对于不同的 $k$ 作为一个一个点 $\vec{x}^{T} \in \mathbb{R}^{2}$ 的 representation. *i.e.* $\vec{x} = (x_1, x_2, x_3)^{T} \in \mathbb{P}^{2} \equiv (\frac{x_1}{x_3}, \frac{x_2}{x_3})^{T} \in \mathbb{R}^{2}$

**一个概念：Degree of freedom (dof) 自由度**：A point has $2$ dof : x and y coordinates; a line has $2$ dof: two independent ratios: $\{ a:b:c\}$

### Intersection of Lines

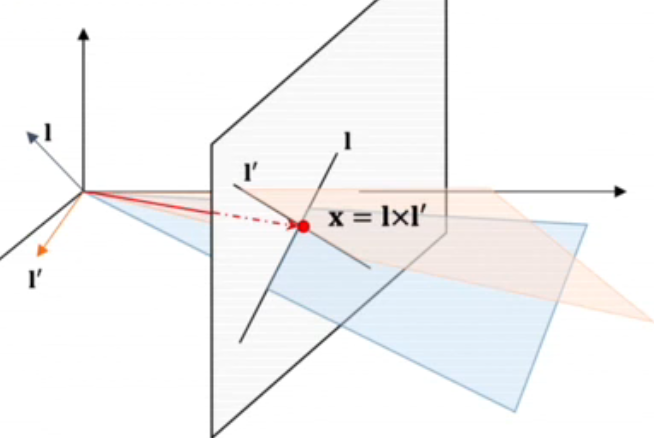![Screenshot 2024-08-30 003613.png](https://s1.locimg.com/2024/08/30/45b698428168b.png)

- 两条线 $\vec{l}$ 和 $\vec{l'}$的交是一个点 $\vec{x} = \vec{l} \times \vec{l'}$

## Line Joining Points

- 换个角度来说，两个点的叉积又是过两个点的直线 $\vec{l} = \vec{x} \times \vec{x'}$

### Ideal Points and the Line at infinity

**Intersection of two parallel lines**

- 考虑两条平行线：$ax+by+c=0$ 和 $ax+by+c' =0 $ 即 $\vec{l} = (a,b,c)$ 和 $\vec{l'} = (a, b, c')$
- 他们的交点为 $\vec{x} = \vec{l} \times \vec{l'} = (c'-c)(b, -a, 0)^{T}$ *i.e.* 忽略 scalar $(c'-c)$
- 会发现 $(b,-a,0)^{T}$ 是两条平行线的交点 $k = 0$ 指出了他们在无限远处相交

最后修改：2024 年 08 月 30 日