多元线性回归的梯度下降算法和标准化操作

博主： tony102
发布时间：2023 年 08 月 10 日
838 次浏览
暂无评论
5675字数
分类：机器学习

## 前言

其实相当简单，只是在一元的基础上多增加了几个维度。

## 多元线性回归

以预测房价为例。我们现在有一些数据

| Size (sqft) | Number of Bedrooms | Number of floors | Age of  Home | Price (1000s dollars) |
| ------------- | -------------------- | ------------------ | -------------- | ----------------------- |
| 952         | 2                  | 1                | 65           | 271.5                 |
| 1244        | 3                  | 2                | 64           | 232                   |
| 1947        | 3                  | 2                | 17           | 509.8                 |
| ...         | ...                | ...              | ...          | ...                   |

现在我们不仅仅只有房子的面积来对应一个价格了，而是说，我们对一套房子有几个**维度**的信息来对应一个价格

我们记这些数据分别为 $x_0, x_1, \dots, x_{n-1}$，每个数据都包含了 $m$ 个维度 $y_j$，那么我们对于第 $i \in [0,n)$ 组数据，我们都要确定一个 $w_i$。

我们可以把数据写做一个 $n \times m$ 的矩阵，记为 $X$，那么 $X$ 形如下：

$$
\mathbf{X} = 
\begin{pmatrix}
 x^{(0)}_0 & x^{(0)}_1 & \cdots & x^{(0)}_{n-1} \\ 
 x^{(1)}_0 & x^{(1)}_1 & \cdots & x^{(1)}_{n-1} \\
 \cdots \\
 x^{(m-1)}_0 & x^{(m-1)}_1 & \cdots & x^{(m-1)}_{n-1} 
\end{pmatrix}

同时，我们把求得 $w_i$ 写成一个列向量:

$$
\mathbf{w} = \begin{pmatrix}
w_0 \\ 
w_1 \\
\cdots\\
w_{n-1}
\end{pmatrix}

而我们 $f_{w,b}$ 中的 $b$ 是一个标量。

那么我们现在就可以得到我们现在的回归函数：

$$
f_{\mathbf{w},b}(\mathbf{x}) =  w_0x_0 + w_1x_1 +... + w_{n-1}x_{n-1} + b \tag{1}

如果写成向量的形式就是：

$$
f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w} \cdot \mathbf{x} + b  \tag{2}

同理，我们只要对每一个维度进行偏微分即可，如下：

$$
\begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\;

& w_j := w_j -  \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1}  \; & \text{for j = 0..n-1}\newline

&b\ \ := b -  \alpha \frac{\partial J(\mathbf{w},b)}{\partial b}  \newline \rbrace

\end{align*}

$$
\begin{align}

\frac{\partial J(\mathbf{w},b)}{\partial w_j}  &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \tag{2}  \\

\frac{\partial J(\mathbf{w},b)}{\partial b}  &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{3}

\end{align}

所以就是很简单的东西，只是稍微拓展了一下。

## `numpy.dot()` 的优化计算

注意到，当我们无论是对每一个维度算 $J(w,b)$ 还是说算偏微分的时候，我们实际上都是进行了一个向量的数乘操作。

一般的写法是用一个循环来计算，但是 `numpy.dot()` 提供了一个更加高效的计算方式。具体不多阐述。

小插曲：买了一个有 GPU 的笔电，就很想用 GPU 来优化计算。然后又是搞 CUDA，又是搞 3060 的驱动，然后还发现了一个叫做 cupy 的东西。按照说法是跟 numpy 的语法一模一样的，然后会自动搞成 CUDA 计算。很高端。但是最后的结果是桌面系统被破坏，然后重装了一遍 Ubuntu

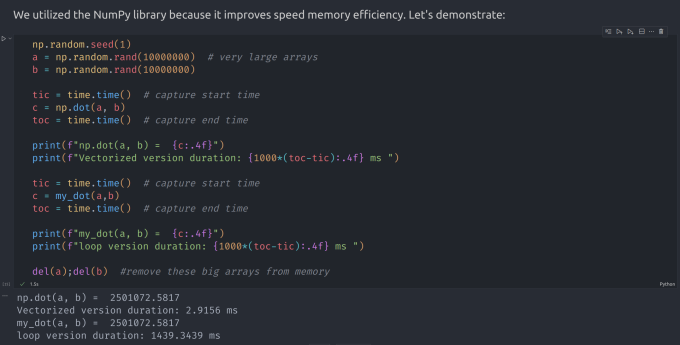[![pPmUnxS.md.png](https://tony102.com/usr/uploads/2023/08/1347521459.png)](https://imgse.com/i/pPmUnxS)

具体效果可以看到，两者差异达到了 700 倍！

## 标准化操作

注意到，由于我们的学习率是比较小的一个数，意味着我们每次下降的不会太多。但是如果我们在每个维度下，数据的差异导致该维度的值域非常大，那么我们不得不增加迭代次数来保证精度。

因此我们希望，我们的值域能够尽可能的集中在某一个值的附近不会太多。一般来说，我们选取 $0$ 作为这个中心。希望数据尽可能集中在 $[-1,1]$ 这样较小的区间内。

#### 均值标准化

均值标准化的操作是这样的，对于每一个 $x_i$ :

$$
x_i := \dfrac{x_i - \mu_i}{max - min}

其中 $\mu_i$ 是该维度各组数据的平均值。

#### z-score 标准化

我的中文翻译：正态分布标准化

正态标准化可以使数据分布的类似于一个钟形的正态分布曲线。这样子很有利于一方面减少迭代次数，一方面提高精度。

具体地，

$$
x^{(i)}_j = \dfrac{x^{(i)}_j - \mu_j}{\sigma_j} \tag{4}

$$
\begin{align}
\mu_j &= \frac{1}{m} \sum_{i=0}^{m-1} x^{(i)}_j \tag{5}\\
\sigma^2_j &= \frac{1}{m} \sum_{i=0}^{m-1} (x^{(i)}_j - \mu_j)^2  \tag{6}
\end{align}

其中 $\mu_j, \sigma_j$ 的含义正如各位学习正态分布时的学习的含义。

## 代码

```python
import numpy as np
import copy

def read():
    def get_numbers():
        try:
            read.s = input().split()
            read.s_len = len(read.s)
            if(read.s_len == 0):get_numbers()
            read.cnt = 0
            return 1
        except:
            return 0
    if not hasattr(read, 'cnt'):
        if not get_numbers():return 0
    if read.cnt == read.s_len:
        if not get_numbers():return 0
    read.cnt += 1
    return eval(read.s[read.cnt-1])

def readin():
    data = np.loadtxt("./data/houses.txt", delimiter = ',', skiprows = 1)
    x_in = data[:, :4]
    y_in = data[:, 4]
    return x_in, y_in

def calcCost(x, y, w, b):
    m = x.shape[0]
    cost = 0.0
    for i in range(m):
        f_i = np.dot(x[i], w) + b
        cost = cost + (f_i - y[i]) ** 2
    cost = cost / (2.00 * m)
    return cost

def calcGradient(x, y, w, b):
    m, n = x.shape
    dw = np.zeros((n, )); db = 0.00
    for i in range(m):
        err = (np.dot(x[i], w) + b) - y[i]
        for j in range(n):
            dw[j] = dw[j] + err * x[i, j]
        db = db + err
    dw = dw / m; db = db / m
    return dw, db

def gradientRegression(x, y, w_ini, b_ini, dep, alpha):
    w = copy.deepcopy(w_ini)
    b = b_ini
    for t in range(dep):
        dw, db = calcGradient(x, y, w, b)
        w = w - alpha * dw; b = b - alpha * db
    return w, b

def z_score_normalization(x):
    mu = np.mean(x, axis = 0)
    sigma = np.std(x, axis = 0)
    x_norm = (x - mu) / sigma
    return (x_norm, mu, sigma)

def run(x, y, alpha = 5e-3, dep = int(1e4)):
    m, n = x.shape
    w_ini = np.zeros(n)
    b_ini = 0
    return gradientRegression(x, y, w_ini, b_ini, dep, alpha)

def query(w, b):
    house = np.arange(4)
    for i in range(4):
        house[i] = read()
    house_norm, house_mu, house_sigma = z_score_normalization(house)
    price_prediction = np.dot(house_norm, w) + b
    print(f"Your house with {house[0]} sqft, {house[1]} bedrooms, {house[2]} floors, {house[3]} years old = {price_prediction:0.1f}K$")

def main():  
    x_train, y_train = readin()
    x_norm, x_mu, x_sigma = z_score_normalization(x_train)
    w, b = run(x_norm, y_train)
    q = read()
    for t in range(q):
        query(w, b)
main()
```

最后修改：2023 年 08 月 14 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

CJ_S00021
我是真的zhouhaoxu，声明一下我不是张清的，我是他的npy。
CJ_zhouhaoxu
我是真的S00021，说两句，第一，我是张青的星怒；第二，第一...
看透一切的大黄
⌇●﹏●⌇
观月
受益匪浅
Harkerbest
好好好

PKUSC2021 Day2
评论数： 0
点和向量的旋转
评论数： 0
20211103 并王 (bing)
评论数： 0
CF86D Powerful array
评论数： 0
AC 自动机总结
评论数： 0

多元线性回归的梯度下降算法和标准化操作

tony102 • 2023 年 08 月 10 日

## 前言

其实相当简单，只是在一元的基础上多增加了几个维度。

## 多元线性回归

以预测房价为例。我们现在有一些数据

现在我们不仅仅只有房子的面积来对应一个价格了，而是说，我们对一套房子有几个**维度**的信息来对应一个价格

我们记这些数据分别为 $x_0, x_1, \dots, x_{n-1}$，每个数据都包含了 $m$ 个维度 $y_j$，那么我们对于第 $i \in [0,n)$ 组数据，我们都要确定一个 $w_i$。

我们可以把数据写做一个 $n \times m$ 的矩阵，记为 $X$，那么 $X$ 形如下：

同时，我们把求得 $w_i$ 写成一个列向量:

$$
\mathbf{w} = \begin{pmatrix}
w_0 \\ 
w_1 \\
\cdots\\
w_{n-1}
\end{pmatrix}

而我们 $f_{w,b}$ 中的 $b$ 是一个标量。

那么我们现在就可以得到我们现在的回归函数：

$$
f_{\mathbf{w},b}(\mathbf{x}) =  w_0x_0 + w_1x_1 +... + w_{n-1}x_{n-1} + b \tag{1}

如果写成向量的形式就是：

$$
f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w} \cdot \mathbf{x} + b  \tag{2}

同理，我们只要对每一个维度进行偏微分即可，如下：

$$
\begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\;

& w_j := w_j -  \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1}  \; & \text{for j = 0..n-1}\newline

&b\ \ := b -  \alpha \frac{\partial J(\mathbf{w},b)}{\partial b}  \newline \rbrace

\end{align*}

$$
\begin{align}

\frac{\partial J(\mathbf{w},b)}{\partial w_j}  &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \tag{2}  \\

\frac{\partial J(\mathbf{w},b)}{\partial b}  &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{3}

\end{align}

所以就是很简单的东西，只是稍微拓展了一下。

## `numpy.dot()` 的优化计算

注意到，当我们无论是对每一个维度算 $J(w,b)$ 还是说算偏微分的时候，我们实际上都是进行了一个向量的数乘操作。

一般的写法是用一个循环来计算，但是 `numpy.dot()` 提供了一个更加高效的计算方式。具体不多阐述。

[![pPmUnxS.md.png](https://tony102.com/usr/uploads/2023/08/1347521459.png)](https://imgse.com/i/pPmUnxS)

具体效果可以看到，两者差异达到了 700 倍！

## 标准化操作

#### 均值标准化

均值标准化的操作是这样的，对于每一个 $x_i$ :

$$
x_i := \dfrac{x_i - \mu_i}{max - min}

其中 $\mu_i$ 是该维度各组数据的平均值。

#### z-score 标准化

我的中文翻译：正态分布标准化

正态标准化可以使数据分布的类似于一个钟形的正态分布曲线。这样子很有利于一方面减少迭代次数，一方面提高精度。

具体地，

$$
x^{(i)}_j = \dfrac{x^{(i)}_j - \mu_j}{\sigma_j} \tag{4}

$$
\begin{align}
\mu_j &= \frac{1}{m} \sum_{i=0}^{m-1} x^{(i)}_j \tag{5}\\
\sigma^2_j &= \frac{1}{m} \sum_{i=0}^{m-1} (x^{(i)}_j - \mu_j)^2  \tag{6}
\end{align}

其中 $\mu_j, \sigma_j$ 的含义正如各位学习正态分布时的学习的含义。

## 代码

```python
import numpy as np
import copy

def readin():
    data = np.loadtxt("./data/houses.txt", delimiter = ',', skiprows = 1)
    x_in = data[:, :4]
    y_in = data[:, 4]
    return x_in, y_in

def z_score_normalization(x):
    mu = np.mean(x, axis = 0)
    sigma = np.std(x, axis = 0)
    x_norm = (x - mu) / sigma
    return (x_norm, mu, sigma)

def run(x, y, alpha = 5e-3, dep = int(1e4)):
    m, n = x.shape
    w_ini = np.zeros(n)
    b_ini = 0
    return gradientRegression(x, y, w_ini, b_ini, dep, alpha)

多元线性回归的梯度下降算法和标准化操作

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

名人传

VP: AtCoder Beginner Contest 222(ABC222)

写在 CSP-S2021 前

机房标准化岚语发音对照

VP: AtCoder Beginner Contest 221(ABC221)

PKUSC2021 Day2

点和向量的旋转

20211103 并王 (bing)

CF86D Powerful array

AC 自动机总结

多元线性回归的梯度下降算法和标准化操作

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

多元线性回归的梯度下降算法和标准化操作

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款