导数大题一类参数估计问题的方法

博主： tony102
发布时间：2022 年 06 月 06 日
492 次浏览
暂无评论
3386字数
分类：总结

## 摘要

有一类导数大题，会带一个参数，让你求这个参数的最大整数值。例如这一次 2022 二模试卷的导数大题第二问就是这种题目。

如果直接含参讨论，会非常痛苦。而且思路并不是很自然。本文介绍一种方法，迅速解决这种问题并获得较高分数。

## 关键词

隐零点；含参问题

## 思路

泰勒展开为我们进行函数估值提供了极强有力的工具。意识到这类题目实际上也是让我们估计参数的值（因为只要你取整），我们考虑应用这类方法。

直接上你并不需要掌握泰勒展开公式，高考考查的函数都是初等函数。平常老师教的放缩就是用泰勒公式做出来的。

考虑到手算的精度有限，因此直接对参变分离后的函数直接替换会有极大的误差直接得到错误答案，我们应该对它的导数进行替换，求到一个较为接近隐零点的 ”假隐零点“，对原函数极值进行估算。

## 前置知识

### 泰勒展开公式（麦克劳林级数）

实际上，基本不会遇到在除 $0$ 处以外的地方展开的题目。因此你可以直接在认为这里介绍的是麦克劳林级数。

$$
f(x) = \sum\limits_{i=0}^{\infty} \frac{f^{(i)}(0)}{i!} x^i
$$

### 常见替换

多项式函数不需要替换。以下无特殊说明均在 $x\geq 0$ 上成立。

指数、对数类

$e^x \geq x+1$  $e^x \geq \frac{x^2}{2} + x + 1$

$\ln(x) \leq x - 1$ $\ln(1+x) = x - \frac{x^2}{2}$

三角函数类：

$\sin(x) \leq x$ $\sin(x) \geq x - \frac{x^3}{3}$

$\cos(x) \geq 1 - \frac{x^2}{2}$

## 例题1：长郡中学 2022 年高三二模第 22 题

### 题面

已知 $f(x)=e^x-ax+\sin^2x$ ，其中 $a\in R, e \approx 2.71828$ 为自然对数的底数。

（1）设曲线 $y=f(x)$ 在点 $(0,f(0))$ 的切线为 $l$ ，若 $l$ 与两坐标轴所围成的三角形的面积为 $\frac{1}{2}$ ，求实数 $a$ 的值

（2）若 $a \in N^{+}$，当 $x \geq 0$ 时，$f(x) \geq 0$ 恒成立，求 $a$ 的最大值。

### 分析

#### 第一问

注意一下算长度的时候是带了绝对值的，注意讨论。$a$ 会有两个取值。

#### 第二问

标准答案的方法非常复杂，我也不会。下面介绍利用该方法进行解答。

以下默认定义域 $x > 0$

通过参变分离得到：$a = F(x) = \frac{e^x+\sin^2(x)}{x}$

求导可得：$F'(x) = \frac{x(e^x+\sin2x)-(e^x+\sin^2x)}{x^2}$

发现这 $F'(x)$  只有一个隐零点。此时构造：$e^x \geq x+1,\sin2x \leq 2x, \sin^2 x \leq x ^ 2$

替换后可得：$F(x) \approx \phi(x) = \frac{2x^2-1}{x^2}$ 在 $x$ 一个较接近 $0$ 的范围的时候（因为后面 $e^x$ 增长远远快于 $x^2$）

令 $\phi(x) = 0 \Longrightarrow x_0 = \frac{1}{\sqrt{2}}$

可得：$F(x_0) \approx 3.7$

所以  $a \leq F(x_0) = 3.7$

实际上，$3.7$ 是手算精度较低的情况下可以快速计算得一个结果实际上结果非常精确（是 $3.46$，误差在 $0.05$ 内。) 如图

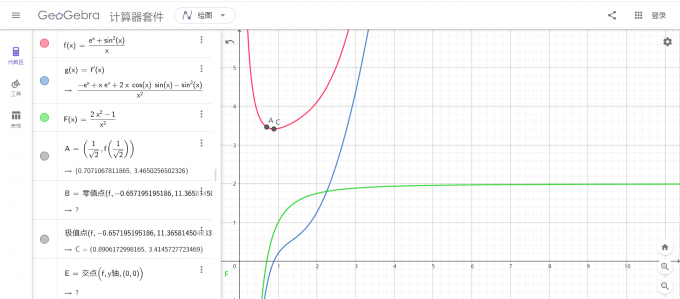[![XBA4KI.md.png](https://tony102.com/usr/uploads/2022/06/4004866125.png)](https://imgtu.com/i/XBA4KI)

## 例题2：长郡 2020 级高水节实验班导数专题第 3 题

### 题面

已知函数 $f(x) = (a-x-1)e^x+x^2-4x-a$

（1）当 $a=4$ 时，求 $f(x)$ 的单调区间。

（2）若不等式 $f(x) \leq (x-2)^2$ 对 $\forall x \in (0,+\infty)$ 恒成立，求实数 $a$ 的最大整数值。

### 分析

第一问不说了。也许你会说，这一个为什么还要单独拎出来说呢？因为这一题的函数性质与上一题大不相同

先参变分离得到：$a\leq F(x) = \frac{e^x(x+1)+4}{e^x-1}$

求导得：$F'(x) = \frac{e^{2x}-6e^x-xe^x}{e^{2x}-2e^x+1}$

下面开始不一样了

#### 采用二阶麦克劳林级数

也就是利用 $e^x \geq x+1$

代入得到：$F'(x) \approx \frac{-5(x+1)}{x^2}$

令 $F'(x_0) = 0 \Longrightarrow x_0 = -1$ 。 $x_0$ 不在定义域内，舍去。

#### 采用三阶麦克劳林级数

很巧的是，上面的二次方项被抵消了。只能硬着头皮上三阶。

不要慌，稍有代数功底的同学们一定会把函数当变量，等化简了以后再来看效果。就像这样：

令 $h(x) = \frac{x^2}{x}+x+1$

那么 $F'(x) \approx \frac{h^2(x) - (x+6)h(x)}{h^2(x)- 2h(x)+1}$

分母是我们不需要关注的。分子恰恰是一个非常好看的形式！

令 $F'(x) = 0$，即使 $h(x)[h(x) -(x+6)] = 0$

因为 $h(x) > 0 $ 恒成立，故只有可能 $h(x) - (x+6) = 0 $。即：$\frac{x^2}{2} - 5 = 0$

解得：$x_0 = \sqrt{10} \approx 3$

代入得：$F(x_0 \approx 3) = 4.4$

所以 $a$ 的最大整数值为 $4$

实际如图：

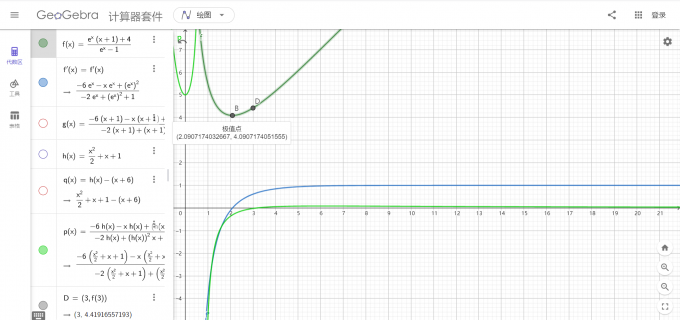[![XBVDAK.md.png](https://tony102.com/usr/uploads/2022/06/2471353845.png)](https://imgtu.com/i/XBVDAK)

图中 $B$ 点是真正的最小值点，求得 $F(3) \approx 4.4$ 。精度也很不错。

## 注意事项

有几个需要重点注意的事情。

**最重要的事情：如果实在没时间了直接放缩阅卷老师是看的懂的你的不等式的，直接写易知往里面带就行。一般会扣 2 分。时间稍微充裕就花 1 分钟证明一下。**

实测二模没有证明那三个不等式只扣了 $2$ 分。性价比还是很不错的。只花了不到 3 分钟就秒解了。

还有一些建议是**蛋哥**看了之后给出来的，衷心感谢他！这些步骤最好加上，毕竟这是来自前高考阅卷组长、备课组长的建议！

1. 最好说明在零点左边导函数小于 $0$ （即零点为变号零点）
2. 检查零点是否唯一。若不唯一，有可能两个都是去极小值的零点，此时需要比较两个极小值的更小值。

一般是不会有第二个建议所述的情况，第一个可以检查一下。

## 经验

指数函数增长的很快，因为不确定隐零点的位置，可以先估计一下。如果离 $x=0$ 比较远一定要用三阶或者更高阶的泰勒展开，否则很容易错。时间充裕建议检查一下相邻的整数值是否可以使不等式成立。

## 写在文末

转眼间我已经从一个 OI 博主转变成高考博主了。

最后修改：2022 年 06 月 07 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

看透一切的人士
催更名人传
看透一切的人士
催更
tham
催更！！！！
wyzwyz
建议把从“小有名气的贫僧”之后的全删了，包括我这句，前面都是一...
潜心学习的打工人
催更

导数大题一类参数估计问题的方法

tony102 • 2022 年 06 月 06 日

## 摘要

有一类导数大题，会带一个参数，让你求这个参数的最大整数值。例如这一次 2022 二模试卷的导数大题第二问就是这种题目。

如果直接含参讨论，会非常痛苦。而且思路并不是很自然。本文介绍一种方法，迅速解决这种问题并获得较高分数。

## 关键词

隐零点；含参问题

## 思路

泰勒展开为我们进行函数估值提供了极强有力的工具。意识到这类题目实际上也是让我们估计参数的值（因为只要你取整），我们考虑应用这类方法。

直接上你并不需要掌握泰勒展开公式，高考考查的函数都是初等函数。平常老师教的放缩就是用泰勒公式做出来的。

## 前置知识

### 泰勒展开公式（麦克劳林级数）

实际上，基本不会遇到在除 $0$ 处以外的地方展开的题目。因此你可以直接在认为这里介绍的是麦克劳林级数。

$$
f(x) = \sum\limits_{i=0}^{\infty} \frac{f^{(i)}(0)}{i!} x^i
$$

### 常见替换

多项式函数不需要替换。以下无特殊说明均在 $x\geq 0$ 上成立。

指数、对数类

$e^x \geq x+1$  $e^x \geq \frac{x^2}{2} + x + 1$

$\ln(x) \leq x - 1$ $\ln(1+x) = x - \frac{x^2}{2}$

三角函数类：

$\sin(x) \leq x$ $\sin(x) \geq x - \frac{x^3}{3}$

$\cos(x) \geq 1 - \frac{x^2}{2}$

## 例题1：长郡中学 2022 年高三二模第 22 题

### 题面

已知 $f(x)=e^x-ax+\sin^2x$ ，其中 $a\in R, e \approx 2.71828$ 为自然对数的底数。

（1）设曲线 $y=f(x)$ 在点 $(0,f(0))$ 的切线为 $l$ ，若 $l$ 与两坐标轴所围成的三角形的面积为 $\frac{1}{2}$ ，求实数 $a$ 的值

（2）若 $a \in N^{+}$，当 $x \geq 0$ 时，$f(x) \geq 0$ 恒成立，求 $a$ 的最大值。

### 分析

#### 第一问

注意一下算长度的时候是带了绝对值的，注意讨论。$a$ 会有两个取值。

#### 第二问

标准答案的方法非常复杂，我也不会。下面介绍利用该方法进行解答。

以下默认定义域 $x > 0$

通过参变分离得到：$a = F(x) = \frac{e^x+\sin^2(x)}{x}$

求导可得：$F'(x) = \frac{x(e^x+\sin2x)-(e^x+\sin^2x)}{x^2}$

发现这 $F'(x)$  只有一个隐零点。此时构造：$e^x \geq x+1,\sin2x \leq 2x, \sin^2 x \leq x ^ 2$

替换后可得：$F(x) \approx \phi(x) = \frac{2x^2-1}{x^2}$ 在 $x$ 一个较接近 $0$ 的范围的时候（因为后面 $e^x$ 增长远远快于 $x^2$）

令 $\phi(x) = 0 \Longrightarrow x_0 = \frac{1}{\sqrt{2}}$

可得：$F(x_0) \approx 3.7$

所以  $a \leq F(x_0) = 3.7$

实际上，$3.7$ 是手算精度较低的情况下可以快速计算得一个结果实际上结果非常精确（是 $3.46$，误差在 $0.05$ 内。) 如图

[![XBA4KI.md.png](https://tony102.com/usr/uploads/2022/06/4004866125.png)](https://imgtu.com/i/XBA4KI)

## 例题2：长郡 2020 级高水节实验班导数专题第 3 题

### 题面

已知函数 $f(x) = (a-x-1)e^x+x^2-4x-a$

（1）当 $a=4$ 时，求 $f(x)$ 的单调区间。

（2）若不等式 $f(x) \leq (x-2)^2$ 对 $\forall x \in (0,+\infty)$ 恒成立，求实数 $a$ 的最大整数值。

### 分析

第一问不说了。也许你会说，这一个为什么还要单独拎出来说呢？因为这一题的函数性质与上一题大不相同

先参变分离得到：$a\leq F(x) = \frac{e^x(x+1)+4}{e^x-1}$

求导得：$F'(x) = \frac{e^{2x}-6e^x-xe^x}{e^{2x}-2e^x+1}$

下面开始不一样了

#### 采用二阶麦克劳林级数

也就是利用 $e^x \geq x+1$

代入得到：$F'(x) \approx \frac{-5(x+1)}{x^2}$

令 $F'(x_0) = 0 \Longrightarrow x_0 = -1$ 。 $x_0$ 不在定义域内，舍去。

#### 采用三阶麦克劳林级数

很巧的是，上面的二次方项被抵消了。只能硬着头皮上三阶。

不要慌，稍有代数功底的同学们一定会把函数当变量，等化简了以后再来看效果。就像这样：

令 $h(x) = \frac{x^2}{x}+x+1$

那么 $F'(x) \approx \frac{h^2(x) - (x+6)h(x)}{h^2(x)- 2h(x)+1}$

分母是我们不需要关注的。分子恰恰是一个非常好看的形式！

令 $F'(x) = 0$，即使 $h(x)[h(x) -(x+6)] = 0$

因为 $h(x) > 0 $ 恒成立，故只有可能 $h(x) - (x+6) = 0 $。即：$\frac{x^2}{2} - 5 = 0$

解得：$x_0 = \sqrt{10} \approx 3$

代入得：$F(x_0 \approx 3) = 4.4$

所以 $a$ 的最大整数值为 $4$

实际如图：

[![XBVDAK.md.png](https://tony102.com/usr/uploads/2022/06/2471353845.png)](https://imgtu.com/i/XBVDAK)

图中 $B$ 点是真正的最小值点，求得 $F(3) \approx 4.4$ 。精度也很不错。

## 注意事项

有几个需要重点注意的事情。

实测二模没有证明那三个不等式只扣了 $2$ 分。性价比还是很不错的。只花了不到 3 分钟就秒解了。

还有一些建议是**蛋哥**看了之后给出来的，衷心感谢他！这些步骤最好加上，毕竟这是来自前高考阅卷组长、备课组长的建议！

一般是不会有第二个建议所述的情况，第一个可以检查一下。

## 经验

## 写在文末

转眼间我已经从一个 OI 博主转变成高考博主了。

导数大题一类参数估计问题的方法

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

名人传

VP: AtCoder Beginner Contest 222(ABC222)

写在 CSP-S2021 前

机房标准化岚语发音对照

VP: AtCoder Beginner Contest 221(ABC221)

Luogu1891 疯狂 LCM

Luogu5513 [CEOI2013]Board

Codechef CTREE Chef and Chefcoin

关于一些题解和讲题

Luogu4248 [AHOI2013]差异

导数大题一类参数估计问题的方法

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

导数大题一类参数估计问题的方法

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款