## 什么是纳什均衡 > 包含两个或以上参与者的非合作博弈(Non-cooperative game)中,假设每个参与者都知道其他参与者的均衡策略的情况下,没有参与者可以透过改变自身策略使自身受益时的一个概念解。 经济学概念?我不懂。社会学?也不懂 OI 中的纳什均衡主要是用来解决一个这样的问题:假如博弈的各方都不知道对方的决策,仅仅依赖于当前自己的最优情况进行决策。且每一方都按照这样的方法进行决策后,每一方的期望收益都不会更多。这样的期望收益点就是纳什均衡点。 其中决策不带概率的被称为:纯策略纳什均衡 (pure strategies);决策有概率的称为:混合策略纳什均衡 (Mixed strategies)。 可能会写一点英文表述,不是我想讲洋文,而是想方便大家看那篇论文的时候快速找到需要看的部分。 形象一点就是这样: 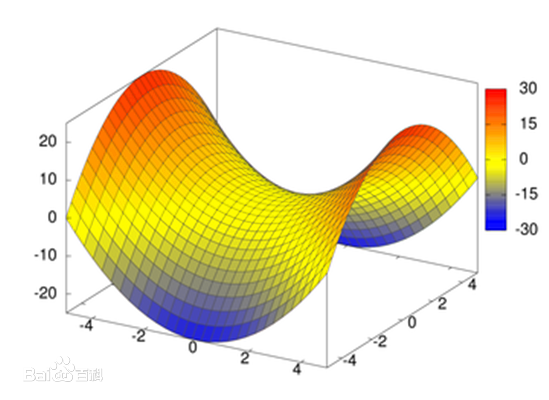 当然,纯策略的纳什均衡肯定是一条直线的。这样有马鞍面的收益期望函数的肯定是混合策略纳什均衡。 注意,这里没有写双方或者多方。实际上,在 [The Complexity of Nash Equilibria](https://tony102.com/archives/195/) 这篇论文中详细介绍了几种纳什均衡的时间复杂度。总的来说,如果是非匿名的多玩家( > 2) 策略为有限集的话,那么这是一个 NP-C 问题。 如果是一个匿名的 n-Players ,策略集大小为 $|k|$ 的一个纳什均衡,则存在近似意义下的多项式时间求解纳什均衡点的算法。应该是 $O(n^k)$ 的算法。(例如 [CF98E](https://tony102.com/archives/192/)) 具体这篇论文只需要看 Chapter 5 的内容即可,其实只看 Chapter 5.1 $\sim$ 5.5 的内容即可。不是很难懂,认真看是可以理解的。关于时间复杂度,稍后再讨论。 主要讨论混合策略的纳什均衡,原因有两点: 1. 纯策略相当于混合策略的一个子集 2. OI 中考察混合策略的题目更加有趣和挑战性 此外,OI 中考察的纳什均衡应均为匿名博弈。 ## 纳什均衡在做什么事 > 如果一个策略组合使任何一个参与人的策略都是相对于其他参与人的策略的最佳策略,这个策略就构成一个纳什均衡,不管这个策略是混合策略还是纯策略。 这是纳什均衡的基础:每个人都选择相对于他人最利自己的策略,当每个人都这样选择并且无法更大任何一人的收益时即达到纳什均衡。 形式化一点可能还好理解一些。以两个人举例。现在有一排蛋糕,Alice 有 $p$ 的概率吃第 $i$ 个,第 $i$ 个蛋糕的美味度是 $a_i$。那么 Alice 的总收益是:$\sum p_ia_i$。当然 Bob 不可能不吃(不吃则 Bob 没有达到相对于 Alice 自身利益最大)。若要达到纳什均衡,也就是 Bob 无论再怎么吃都不可能收获更多美味度。那么最大的肯定是 $\max\limits_{i=1}^{n} {p_ia_i}$ ,这样 Bob 这样吃是最佳的。其它怎么吃都不可能比这个优。因此,Alice 的期望收益(上面的乘了概率 $p_i$ 所有都应该是在期望意义下的)就是 $\sum p_ia_i - \max\limits_{i=1}^{n} {p_ia_i}$ 。Alice 也要自身最优,所以要求 $\max$ 这个式子。 此时有一个结论(下文同样会再次引出),每个参与人的混合策略都使其余参与人的任何纯策略的期望收益相等。所以当 $\forall i, p_ia_i$ 尽可能相当时该式可以得到一个 $\max$ 。 应该大概能看出来,纳什均衡都是在相互之前自利的情况下的最佳策略。并且一个重要结论就是每个参与人的混合策略都使其余参与人的任何纯策略的期望收益相等。这是 OI 中运用纳什均衡解决博弈问题的基础。接下来会继续探讨。 ## 石头剪刀布 现在有两个玩家玩石头剪刀布,我们用 R P S 来分别代表石头、布、剪刀。如果平局收益为 $0$ ,胜一局收益为 $1$ ,负一局收益为 $-1$。 下面通过一个表格来说明这个游戏: | P1\P2 | R | P | S | | :---: | :----: | :----: | :----: | | R | (0,0) | (-1,1) | (1,-1) | | P | (1,-1) | (0,0) | (-1,1) | | S | (-1,1) | (1,-1) | (0,0) | 我们设两人都有 $p_1, p_2, p_3$ 的概率出 R,P,S. 那么若要达到纳什均衡,则应该两人的混合策略都使对方的纯策略期望收益相等,也就是: $-1 \cdot p_2 + p_3 = -1 \cdot p_3 + p_1 = -1 \cdot p_1 + p_2$ 为了强调 $1/-1$ 所以符号为负的项都写在了前面。可以解得上面的方程组的为:$p_1 = p_2 = p_3 = \frac{1}{3}$。也就是说,在纳什均衡的意义下,双方应等概率随机出 R,P,S 从这个例子,也能看出来,解混合策略纳什均衡可以令参与人的各个纯策略收益相等,构成方程组求解。 ## 一个让人感叹书读少了的例子 摸鱼一下,这个道理还是很深刻的。且不谈这个例子的严谨性(基本正确),但还是现实意义沉重。 > 如果你喜欢一个女孩子。现在女孩子把你当很好很好的朋友。 > > 如果你表白,女孩子觉得这样当朋友太尴尬了,那以后可能一起玩的机会都没有了。 > > 如果女孩子把你拒绝了,她也就失去了一个很好的朋友,这一点对现在的她来说也不是好的结果。 > > 于是你们俩,谁都不愿主动做出改变,即纳什均衡。 > > 你们俩在信息不完全下达到了各自的最优。但对于外人来看却不是。 作者:Ciel 链接:https://www.zhihu.com/question/19804990/answer/154928632 来源:知乎 ## 例题1:CF98E 单独写了题解,直接丢链接:[CF98E](https://tony102.com/archives/192/) ## 例题2:20211108 游戏 (game) 单独写了题解,直接丢链接:[20211108 游戏 (game)](https://tony102.com/archives/196/) ## 再探时间复杂度 开头已经说过了,非匿名的纳什均衡点求解是 NP-C 的。下面均值讨论有限策略集的匿名纳什均衡点求解。 首先什么样的博弈是匿名博弈。**不可以顾名思义地认为是博弈方不带名字就是匿名,而是博弈方的收益仅取决于他的策略,而不取决于他的身份**。例如,司机造成的延误取决于路线上的汽车数量,而不是司机的身份。另一个例子如在拍卖中,其中一个出价人的效用受其他出价人出价的分布影响,但不受其他出价人身份的影响。 结论开头已经给出:匿名的 n-Players ,策略集大小为 $|k|$ 的一个纳什均衡,求解均衡点的复杂度是 $O(n^k)$。具体证明在原论文中:Chapter 5.2 介绍了匿名博弈,Chapter 5.3 定义了本章所有符号和定义。Chapter 5.4 主要证明了该结论。后面的章节可能意义就不大了。下面来简要介绍原论文的论述。 首先给出了一个解决纳什均衡点的基本操作:我们并非要直接求这个点,而是求选择每一个策略的概率 $p_i$。设 $z$ 是一个足够大的自然数,那么每一个 $p_i$ 都是 $z$ 的整数倍。我们可以用动态规划来求解这个概率 $p_i$ 。事实上,每个玩家一共有不超过 $(z+1)^{k-1}$ 中策略集,所以 $n$ 个玩家划分这些方案的数量最多是 $n^{(z+1)^{k-1} - 1}$ 。然后比较最大的即可。 原论文指引回了 Chapter 5.1 中的一些结论,可以了解一下。不多赘述。 这样一来,你感觉 CF98E 就是一道跟着论文走的题。 ## 通解 其实通过上面的描述,已经可以感受到在 OI 中纳什均衡的的求法了。**再次强调,我们仅可以解决匿名博弈下的纳什均衡点。** 通过 dp / 记忆话搜索都可以做划分数 dp,dp 的状态就是划分。转移的时候做如下步骤: 1. 计算当前状态下的纳什均衡点 $p$ 2. 根据 $p$ 点算出当前状态的最大期望收益 这样大概就是纳什均衡在 OI 中的一般运用了。(主要纳什均衡的题目实在是太少了,几乎没有) 如果是纯策略的话,直接求解线性方程组了。 ## 线性空间与纳什均衡 纯策略的时候相当于最有期望可以被一条直线所表示,我们要做的是解方程组。 那么混合策略的时候是不是也有类似的性质呢? 当然是有的,在论文中证明复杂度的时候就是把策略看成一个 $k$ 维向量。当然,因为这跟解题没啥关系,不重要,了解即可。 Loading... ## 什么是纳什均衡 > 包含两个或以上参与者的非合作博弈(Non-cooperative game)中,假设每个参与者都知道其他参与者的均衡策略的情况下,没有参与者可以透过改变自身策略使自身受益时的一个概念解。 经济学概念?我不懂。社会学?也不懂 OI 中的纳什均衡主要是用来解决一个这样的问题:假如博弈的各方都不知道对方的决策,仅仅依赖于当前自己的最优情况进行决策。且每一方都按照这样的方法进行决策后,每一方的期望收益都不会更多。这样的期望收益点就是纳什均衡点。 其中决策不带概率的被称为:纯策略纳什均衡 (pure strategies);决策有概率的称为:混合策略纳什均衡 (Mixed strategies)。 可能会写一点英文表述,不是我想讲洋文,而是想方便大家看那篇论文的时候快速找到需要看的部分。 形象一点就是这样:  当然,纯策略的纳什均衡肯定是一条直线的。这样有马鞍面的收益期望函数的肯定是混合策略纳什均衡。 注意,这里没有写双方或者多方。实际上,在 [The Complexity of Nash Equilibria](https://tony102.com/archives/195/) 这篇论文中详细介绍了几种纳什均衡的时间复杂度。总的来说,如果是非匿名的多玩家( > 2) 策略为有限集的话,那么这是一个 NP-C 问题。 如果是一个匿名的 n-Players ,策略集大小为 $|k|$ 的一个纳什均衡,则存在近似意义下的多项式时间求解纳什均衡点的算法。应该是 $O(n^k)$ 的算法。(例如 [CF98E](https://tony102.com/archives/192/)) 具体这篇论文只需要看 Chapter 5 的内容即可,其实只看 Chapter 5.1 $\sim$ 5.5 的内容即可。不是很难懂,认真看是可以理解的。关于时间复杂度,稍后再讨论。 主要讨论混合策略的纳什均衡,原因有两点: 1. 纯策略相当于混合策略的一个子集 2. OI 中考察混合策略的题目更加有趣和挑战性 此外,OI 中考察的纳什均衡应均为匿名博弈。 ## 纳什均衡在做什么事 > 如果一个策略组合使任何一个参与人的策略都是相对于其他参与人的策略的最佳策略,这个策略就构成一个纳什均衡,不管这个策略是混合策略还是纯策略。 这是纳什均衡的基础:每个人都选择相对于他人最利自己的策略,当每个人都这样选择并且无法更大任何一人的收益时即达到纳什均衡。 形式化一点可能还好理解一些。以两个人举例。现在有一排蛋糕,Alice 有 $p$ 的概率吃第 $i$ 个,第 $i$ 个蛋糕的美味度是 $a_i$。那么 Alice 的总收益是:$\sum p_ia_i$。当然 Bob 不可能不吃(不吃则 Bob 没有达到相对于 Alice 自身利益最大)。若要达到纳什均衡,也就是 Bob 无论再怎么吃都不可能收获更多美味度。那么最大的肯定是 $\max\limits_{i=1}^{n} {p_ia_i}$ ,这样 Bob 这样吃是最佳的。其它怎么吃都不可能比这个优。因此,Alice 的期望收益(上面的乘了概率 $p_i$ 所有都应该是在期望意义下的)就是 $\sum p_ia_i - \max\limits_{i=1}^{n} {p_ia_i}$ 。Alice 也要自身最优,所以要求 $\max$ 这个式子。 此时有一个结论(下文同样会再次引出),每个参与人的混合策略都使其余参与人的任何纯策略的期望收益相等。所以当 $\forall i, p_ia_i$ 尽可能相当时该式可以得到一个 $\max$ 。 应该大概能看出来,纳什均衡都是在相互之前自利的情况下的最佳策略。并且一个重要结论就是每个参与人的混合策略都使其余参与人的任何纯策略的期望收益相等。这是 OI 中运用纳什均衡解决博弈问题的基础。接下来会继续探讨。 ## 石头剪刀布 现在有两个玩家玩石头剪刀布,我们用 R P S 来分别代表石头、布、剪刀。如果平局收益为 $0$ ,胜一局收益为 $1$ ,负一局收益为 $-1$。 下面通过一个表格来说明这个游戏: | P1\P2 | R | P | S | | :---: | :----: | :----: | :----: | | R | (0,0) | (-1,1) | (1,-1) | | P | (1,-1) | (0,0) | (-1,1) | | S | (-1,1) | (1,-1) | (0,0) | 我们设两人都有 $p_1, p_2, p_3$ 的概率出 R,P,S. 那么若要达到纳什均衡,则应该两人的混合策略都使对方的纯策略期望收益相等,也就是: $-1 \cdot p_2 + p_3 = -1 \cdot p_3 + p_1 = -1 \cdot p_1 + p_2$ 为了强调 $1/-1$ 所以符号为负的项都写在了前面。可以解得上面的方程组的为:$p_1 = p_2 = p_3 = \frac{1}{3}$。也就是说,在纳什均衡的意义下,双方应等概率随机出 R,P,S 从这个例子,也能看出来,解混合策略纳什均衡可以令参与人的各个纯策略收益相等,构成方程组求解。 ## 一个让人感叹书读少了的例子 摸鱼一下,这个道理还是很深刻的。且不谈这个例子的严谨性(基本正确),但还是现实意义沉重。 > 如果你喜欢一个女孩子。现在女孩子把你当很好很好的朋友。 > > 如果你表白,女孩子觉得这样当朋友太尴尬了,那以后可能一起玩的机会都没有了。 > > 如果女孩子把你拒绝了,她也就失去了一个很好的朋友,这一点对现在的她来说也不是好的结果。 > > 于是你们俩,谁都不愿主动做出改变,即纳什均衡。 > > 你们俩在信息不完全下达到了各自的最优。但对于外人来看却不是。 作者:Ciel 链接:https://www.zhihu.com/question/19804990/answer/154928632 来源:知乎 ## 例题1:CF98E 单独写了题解,直接丢链接:[CF98E](https://tony102.com/archives/192/) ## 例题2:20211108 游戏 (game) 单独写了题解,直接丢链接:[20211108 游戏 (game)](https://tony102.com/archives/196/) ## 再探时间复杂度 开头已经说过了,非匿名的纳什均衡点求解是 NP-C 的。下面均值讨论有限策略集的匿名纳什均衡点求解。 首先什么样的博弈是匿名博弈。**不可以顾名思义地认为是博弈方不带名字就是匿名,而是博弈方的收益仅取决于他的策略,而不取决于他的身份**。例如,司机造成的延误取决于路线上的汽车数量,而不是司机的身份。另一个例子如在拍卖中,其中一个出价人的效用受其他出价人出价的分布影响,但不受其他出价人身份的影响。 结论开头已经给出:匿名的 n-Players ,策略集大小为 $|k|$ 的一个纳什均衡,求解均衡点的复杂度是 $O(n^k)$。具体证明在原论文中:Chapter 5.2 介绍了匿名博弈,Chapter 5.3 定义了本章所有符号和定义。Chapter 5.4 主要证明了该结论。后面的章节可能意义就不大了。下面来简要介绍原论文的论述。 首先给出了一个解决纳什均衡点的基本操作:我们并非要直接求这个点,而是求选择每一个策略的概率 $p_i$。设 $z$ 是一个足够大的自然数,那么每一个 $p_i$ 都是 $z$ 的整数倍。我们可以用动态规划来求解这个概率 $p_i$ 。事实上,每个玩家一共有不超过 $(z+1)^{k-1}$ 中策略集,所以 $n$ 个玩家划分这些方案的数量最多是 $n^{(z+1)^{k-1} - 1}$ 。然后比较最大的即可。 原论文指引回了 Chapter 5.1 中的一些结论,可以了解一下。不多赘述。 这样一来,你感觉 CF98E 就是一道跟着论文走的题。 ## 通解 其实通过上面的描述,已经可以感受到在 OI 中纳什均衡的的求法了。**再次强调,我们仅可以解决匿名博弈下的纳什均衡点。** 通过 dp / 记忆话搜索都可以做划分数 dp,dp 的状态就是划分。转移的时候做如下步骤: 1. 计算当前状态下的纳什均衡点 $p$ 2. 根据 $p$ 点算出当前状态的最大期望收益 这样大概就是纳什均衡在 OI 中的一般运用了。(主要纳什均衡的题目实在是太少了,几乎没有) 如果是纯策略的话,直接求解线性方程组了。 ## 线性空间与纳什均衡 纯策略的时候相当于最有期望可以被一条直线所表示,我们要做的是解方程组。 那么混合策略的时候是不是也有类似的性质呢? 当然是有的,在论文中证明复杂度的时候就是把策略看成一个 $k$ 维向量。当然,因为这跟解题没啥关系,不重要,了解即可。 最后修改:2021 年 11 月 09 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏