《廊桥分配》问题研究

博主： tony102
发布时间：2021 年 11 月 02 日
1951 次浏览
暂无评论
999字数
分类：题解总结

## 前情提要

菜鸡托在考场上狂写了二分，萎了；三分，萎了；二分+范围暴力（40 + 10)。

对这个题的答案函数到底长成什么样子非常好奇，因为二分三分全部萎了。花了两个小时发现了一些奇妙的事情，很有价值拓展。

这篇 blog 就来分析一下。

## 答案函数

假如我们设国内分配 $x$ 个廊桥的时候，最多停靠 $f(x)$ 次航班，国外的同理有 $g(y)$。我们知道 $x+y=n$。暴力做法是，我们枚举 $x$，然后 $O(n \log (m_1+m_2)) = O(n \log n)$ 地算答案。这样总共是 $O(n^2 \log )$ 的。当 $x$ 单增时，$y$ 单减；同时 $f(x)$ 单调不降，$g(y)$ 单调不增。这样答案就是 $h(x) = f(x) + g(n-x)$

这样的函数到底有单不单峰，答案很显然不单峰。但是假如你跟我一样傻逼，就会先认为它单调再认为它单峰。

随便举一个例子都能 hack 掉这个，例如初等函数中 $\sin, \cos$ 函数都可以 hack 掉这个。

我们枚举每一个 $x$ ，然后把它的 $(x,c_1), (y,c_2)$  打印出来，然后在 Geogebra 上描点绘图。注意不要使用 `polynomial` ，这个东西好像不支持点太多来插值出一个多项式函数。只能用 `Fitpoly`, 后面有一个 `Degree of Polynomial` 的参数可以控制多项式度数。还有一个事情就是，这样我们只能得到整数上的点，所以拟合出来的函数不太准确。所以我在每一个 $[x,x+1]$ 中间都插了三个点，函数值就是四等分。这样让函数比较平滑。性质上也更加准确。

花了很长时间根据样例 3 画了一个图，长这样：

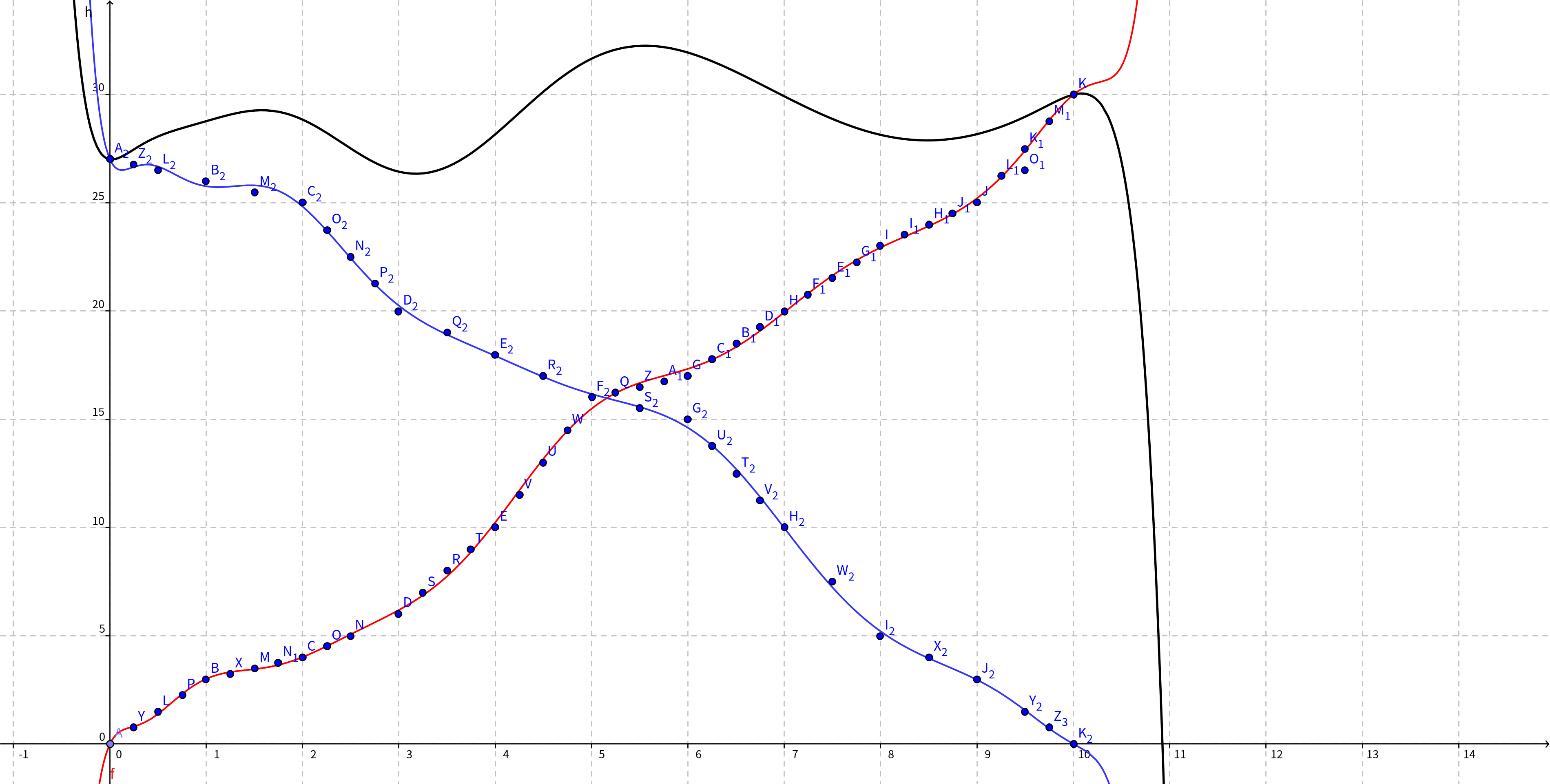![sample](https://tony102.com/usr/uploads/2021/11/1843225884.png)

暴力算答案的代码：

```cpp
int judge(int x) {
	std::priority_queue < int, vector < int >, greater < int > > q;
	int y = n - x; int c1 = 0, c2 = 0;
	for (int i = 1; i <= m1; ++ i) {
		while (!q.empty() && q.top() <= a1[i].l) q.pop();
		if (q.size() + 1 <= x) q.push(a1[i].r), ++ c1;
	}
	while (!q.empty()) q.pop();
	for (int i = 1; i <= m2; ++ i) {
		while (!q.empty() && q.top() <= a2[i].l) q.pop();
		if (q.size() + 1 <= y) q.push(a2[i].r), ++ c2;
	}
	if (ans < c1 + c2) return ans = c1 + c2, 1;
	else return 1;
}
```

明显 $h(x)$ 多峰。如果还是非要利用 $f(x)$ 和 $g(x)$ 单调的性质，可以试试一个 $O(n \log ^3 n)$ 的算法：二分 $x, y$ ，然后 $O(n \log n)$ 检验。可惜并没有这一档分。

## 无聊：多项式

定义 $n$ 为一常量，则：$h(x) = f(x) + g(n-x)$

看到这个式子，你很想卷一下。但是奈何中间是个 $+$ 号，但是没有关系，你知道指数运算可以帮助你：$e^{h(x)} = e^{f(x)} \cdot e^{g(n-x)} = e^{f(x)+g(n-x)}$

然后呢？没有然后了。因为三个函数并不是一个多项式，上面那张图的函数是我们拟合出来的。所以想求出 $e^{h(x)}$ 之后再背包做不了。

纯粹就是我一次失败的尝试（无聊

## 暴力和正解

回头看看上面贴的我的考场暴力代码，不禁感觉这玩意儿怎么跟正解这么像....

假如在 `while (!q.empty() && q.top() <= a1[i].l) q.pop();` 这一句后面把弹出的东西用一个堆把它存下来，后面 `++ c1` 的时候从这个堆里面取，就变成了正解....

看到这里，你不禁再次感叹写这篇 blog 的人是个**大傻逼**。

看看正解中有一段叫做：**求前缀和** 的步骤。

```cpp
for (int i = 0; i <= n; ++ i) ans = std::max(ans, s1[i] + s2[n - i]);
```

想把这个 $s_1, s_2$ 打印出来一探究竟。

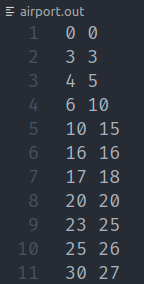![airport](https://tony102.com/usr/uploads/2021/11/921803308.png)

突然你发现，把第二列反转一下，这些就是描点的时候 $f(x), g(x)$ 的值。

日！！！！！！！！！！！！

可能这个时候你已经感受到了一些东西。让我们来理一理这到底是怎么回事。

再次回到 $f(x)$ 和 $g(x)$ 上，$f(x)$ 是怎么算出来的：$f(x-1) + \Delta \to f(x)$。其中 $\Delta$ 在这道题中就是廊桥增多一个，带来的多停靠的航班。

### 再次无聊：有限微积分

嘘~千万不要告诉王总了

当你看到 $f(x-1) + \Delta \to f(x)$ 这个形式的时候，你肯定在纳闷：？，这不是有限微积分？？？

确实，如果你看到绘图的步骤中，为了让这个函数连续平滑，我们在整点之间插了三个点。实际上，$f(x)$ 和 $g(x)$ 都应该是定义在一个离散域上的。

写到这里，在作者的脑海里面这道题所有解法都已经融会贯通了。基本已经可以解释不同代码中不同操作的正确性。例如尹队代码中的离散化操作，就可以用这件事情来解释。之后的步骤，同样可以解释这一个无聊部分中的内容。

继续。你想有限微积分为我们提供了一个求出 $f(n)$ 的方法，但问题是中间坍缩的部分也要能求出来。问题又回到了起点。不过没有关系，很快你就能在接下来的部分中看到这道题影射出的一个方法。

回到正题。此时已经恍然大悟，暴力做法相当于一个 “单点求值” 的操作，而正解实现了求前缀和。关键就在那一个堆上面。想想我们确实是要做一个前缀和的操作，因为每多一个廊桥，而廊桥之间互不影响，之前已经有的廊桥停靠的航班数量肯定要加到新加的这个廊桥的答案上来。看上去我们的做法是在给航班配对廊桥，实际上我们在对廊桥求前缀和。想想每次从那个维护闲置的廊桥中取出一个作为停靠当前枚举的航班的停靠的步骤，相当于这个廊桥原本算前缀和的位置因为题目要求强制让它不能再继续 $+1$ 了，但是后面仍然存在位置可以让它继续算前缀和。所以这个维护闲置廊桥的堆，就是维护了所有合法的前缀位置。

这样一来，就可以完全解决求前缀和的问题。~~有限微积分突然就行了，但其实对这道题没什么用，因为这道题要求的是一个前缀和和后缀和的和最大的位置的答案~~。

实际上，假如我们再打印每个廊桥分别在国内国外区能停靠的航班数，实际上就是 $f(x) - f(x-1) = \Delta$ （再次与王总的有限微积分联系）。这样也可以解释尹队的做法：

> 考虑维护廊桥数为 $i$ 时的答案以及当前剩下来的廊桥数量，对于每个飞机找到其最先的有廊桥的位置，之后就是答案的后缀加，对于答案的处理直接差分+前缀和就行了，而对于剩下的廊桥，仍然考虑差分，就是把差分数组最前面一个 $1$ 变成 $0$ 就行了，直接用堆维护即可。

差分就算出来的是这个 $\Delta$ （有限微积分浅显理解的本质：差分），再求和即得到原函数的值。同样用对维护当前位置最早一个可以转移过来求前缀和的前缀位置。

## 总结

到这里可能已经有一点醍醐灌顶的感觉了。

总而言之，这道题目给了我们一种贪心的套路，像这种 $h(x)$ 函数的最大值问题，我们假如暴力可以单点求出它的值，观察它的组成 $f(x), g(x)$，发现是在做前缀和。那么我们肯定希望当前位置从最早的前缀和加过来，这样可以尽量多加。也就是一种有条件转移的函数前缀和的方法：用堆维护这个前缀位置。

虽然说花了一上午搞清楚这个问题，但是收获颇丰，是吧！

哈希说他三分过了 75，有人三分有 80 还是 100？？？？我考场上 `mt19937` rand 出来的数据都比 CCF 强，因为二分三分全部拍萎了....让我来造数据，三分的同学一分都别想得。

最后修改：2021 年 11 月 02 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

xbieygztgu
不错不错，我喜欢看 https://www.ea55.com/
ojvrnvtsvs
看的我热血沸腾啊https://www.ea55.com/
orzaztmfuh
不错不错，我喜欢看 https://www.ea55.com/
mzcwdjqqxe
不错不错，我喜欢看 https://www.ea55.com/
Yanws
牢师求更新

《廊桥分配》问题研究

tony102 • 2021 年 11 月 02 日

## 前情提要

菜鸡托在考场上狂写了二分，萎了；三分，萎了；二分+范围暴力（40 + 10)。

对这个题的答案函数到底长成什么样子非常好奇，因为二分三分全部萎了。花了两个小时发现了一些奇妙的事情，很有价值拓展。

这篇 blog 就来分析一下。

## 答案函数

这样的函数到底有单不单峰，答案很显然不单峰。但是假如你跟我一样傻逼，就会先认为它单调再认为它单峰。

随便举一个例子都能 hack 掉这个，例如初等函数中 $\sin, \cos$ 函数都可以 hack 掉这个。

花了很长时间根据样例 3 画了一个图，长这样：

![sample](https://tony102.com/usr/uploads/2021/11/1843225884.png)

暴力算答案的代码：

## 无聊：多项式

定义 $n$ 为一常量，则：$h(x) = f(x) + g(n-x)$

看到这个式子，你很想卷一下。但是奈何中间是个 $+$ 号，但是没有关系，你知道指数运算可以帮助你：$e^{h(x)} = e^{f(x)} \cdot e^{g(n-x)} = e^{f(x)+g(n-x)}$

然后呢？没有然后了。因为三个函数并不是一个多项式，上面那张图的函数是我们拟合出来的。所以想求出 $e^{h(x)}$ 之后再背包做不了。

纯粹就是我一次失败的尝试（无聊

## 暴力和正解

回头看看上面贴的我的考场暴力代码，不禁感觉这玩意儿怎么跟正解这么像....

假如在 `while (!q.empty() && q.top() <= a1[i].l) q.pop();` 这一句后面把弹出的东西用一个堆把它存下来，后面 `++ c1` 的时候从这个堆里面取，就变成了正解....

看到这里，你不禁再次感叹写这篇 blog 的人是个**大傻逼**。

看看正解中有一段叫做：**求前缀和** 的步骤。

```cpp
for (int i = 0; i <= n; ++ i) ans = std::max(ans, s1[i] + s2[n - i]);
```

想把这个 $s_1, s_2$ 打印出来一探究竟。

![airport](https://tony102.com/usr/uploads/2021/11/921803308.png)

突然你发现，把第二列反转一下，这些就是描点的时候 $f(x), g(x)$ 的值。

日！！！！！！！！！！！！

可能这个时候你已经感受到了一些东西。让我们来理一理这到底是怎么回事。

再次回到 $f(x)$ 和 $g(x)$ 上，$f(x)$ 是怎么算出来的：$f(x-1) + \Delta \to f(x)$。其中 $\Delta$ 在这道题中就是廊桥增多一个，带来的多停靠的航班。

### 再次无聊：有限微积分

嘘~千万不要告诉王总了

当你看到 $f(x-1) + \Delta \to f(x)$ 这个形式的时候，你肯定在纳闷：？，这不是有限微积分？？？

确实，如果你看到绘图的步骤中，为了让这个函数连续平滑，我们在整点之间插了三个点。实际上，$f(x)$ 和 $g(x)$ 都应该是定义在一个离散域上的。

## 总结

到这里可能已经有一点醍醐灌顶的感觉了。

虽然说花了一上午搞清楚这个问题，但是收获颇丰，是吧！

《廊桥分配》问题研究

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

名人传

VP: AtCoder Beginner Contest 222(ABC222)

写在 CSP-S2021 前

机房标准化岚语发音对照

VP: AtCoder Beginner Contest 221(ABC221)

Luogu3121 [USACO15FEB]Censoring G

CF101D Castle

点和向量的旋转

Min_25 筛

VP: AtCoder Beginner Contest 221(ABC221)

《廊桥分配》问题研究

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

《廊桥分配》问题研究

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款