## 问题引入 给定一棵 $n$ 个点的树,求以每个点为根的子树的重心。 数据范围:$n \leq 2 \times 10^5$ ## 朴素方法 $O(n^2)$ 对每个点求出重心,时间无法承受。 ## 方法一 考虑到重心的性质:一个子树的重心一定在其根节点所在重链上。发现重心的定义等价于重心的最大子树不超过整棵子树的一半,因此直接在重链上向下倍增即可。 时间复杂度:$O(n \log n)$ 代码: ```cpp int get(int x, int rt) { return std::max(siz[rt] - siz[x], siz[son[x]]); } void dfs1(int u) { if (siz[son[u]] <= siz[u] / 2) tag[ctr[u] = u] = 1; for (int i = head[u], v; i; i = edge[i].nxt) { v = edge[i].to; if (v == fa[u]) continue; dfs1(v); int c = ctr[v]; if (ctr[u] || siz[v] <= siz[u] / 2) continue; while (fa[c] && get(c, u) > siz[u] / 2) c = fa[c]; while (fa[c] && get(fa[c], u) <= siz[u] / 2) c = fa[c]; tag[ctr[u] = c] = 1; } } ``` ## 方法二 还想再优秀一点?试图求得 $O(n)$ 的做法。 有一个假的结论,可以让你爆零:重心只有可能是儿子的重心、儿子重心的父亲和它自己。在这些点组成的可能集合中找子树大小最大的。 还有一个假的结论:重链上连续的一段节点的重心也是该重链上连续的一段节点。 这两个结论为什么假掉了,我们可以构造一棵树,使得存在点不是任何子树的重心。如图: 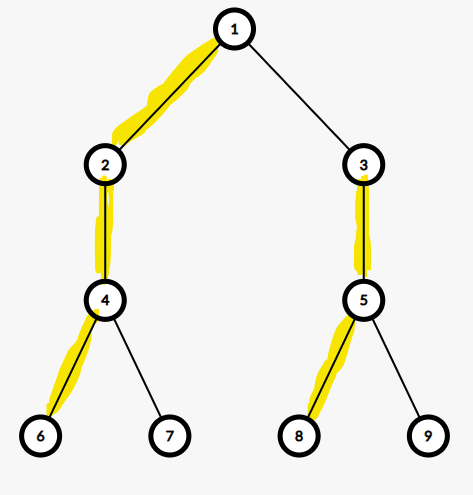 例如在一个应用中,每次修改的点都是重心。 其中标黄的边为重边,未标黄的为轻边。如果我们更新重链上连续的一段:1,2,4。那么对应的需要修改的重心为 1,4。并不是连续的一段。 所以上述结论是假的。 稍微将这个结论换一下就真了:即对于任意节点 $u$ ,以它为重心的节点一定和 $u$ 在同一条重链上并且为连续的一段。 有了这个结论,结合重链的性质:$\sum$ 重链长度 是 $O(n)$ 级别的,我们可以找到 $O(n)$ 做法。 以 20210923 CDQZ NOIp模拟赛中秋特别版 T2为例,代码如下:(by CJ_wyz) ```cpp #include<cstdio> #include<cctype> #include<set> #include<ctime> #include<cmath> #include<queue> #include<vector> #include<bitset> #include<random> #include<cstring> #include<cstdlib> #include<algorithm> #define mp std::make_pair #define swap std::swap #define lowbit(k) (k&(-k)) #define mod 31607 template<class T> inline T read(){ T r=0,f=0; char c; while(!isdigit(c=getchar()))f|=(c=='-'); while(isdigit(c))r=(r<<1)+(r<<3)+(c^48),c=getchar(); return f?-r:r; } template<class T> inline T min(T a,T b){ return a<b?a:b; } template<class T> inline T max(T a,T b){ return a>b?a:b; } #define ll long long inline ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; } inline ll lcm(ll a,ll b){ return a/gcd(a,b)*b; } inline ll qpow(ll a,int b){ ll ans=1; for(;b;b>>=1){ if(b&1)(ans*=a)%=mod; (a*=a)%=mod; } return ans; } #undef ll struct Z{ #define add(x) (x>=mod?x-mod:x) #define sub(x) (x<0?x+mod:x) int x; inline int val() const{ return x; } inline int inv() const{ return qpow(x,mod-2); } Z(int x=0):x(x) {} Z operator -() const{ return Z(add(mod-x)); } Z &operator +=(const Z &z){ x=add(x+z.x); return *this; } Z &operator -=(const Z &z){ x=sub(x-z.x); return *this; } Z &operator *=(const Z &z){ x=1ll*x*z.x%mod; return *this; } Z &operator /=(const Z &z){ x=1ll*x*z.inv()%mod; return *this; } Z operator +(const Z &z) const{ return Z(add(x+z.x)); } Z operator -(const Z &z) const{ return Z(sub(x-z.x)); } Z operator *(const Z &z) const{ return Z(1ll*x*z.x%mod); } Z operator /(const Z &z) const{ return Z(1ll*x*z.inv()%mod); } #undef add #undef sub }; #define maxn 202202 struct E{ int v,nxt; E() {} E(int v,int nxt):v(v),nxt(nxt) {} }e[maxn<<1]; int n,s_e,head[maxn],ct[maxn]; inline void a_e(int u,int v){ e[++s_e]=E(v,head[u]); head[u]=s_e; } int L[maxn],R[maxn]; std::vector<int> d[maxn]; namespace T_C{ int s_dfn,fa[maxn],dfn[maxn],dep[maxn],size[maxn]; int N,low[maxn],down[maxn],top[maxn],son[maxn]; void dfs1(int u){ size[u]=1; dep[u]=dep[fa[u]]+1; for(int i=head[u];i;i=e[i].nxt){ int v=e[i].v; if(size[v])continue; fa[v]=u,dfs1(v); size[u]+=size[v]; if(size[son[u]]<size[v])son[u]=v; } } void dfs2(int u,int t){ top[u]=t; dfn[u]=++s_dfn; d[t].push_back(u); if(!son[u]){ R[u]=s_dfn; return; } dfs2(son[u],t); for(int i=head[u];i;i=e[i].nxt){ int v=e[i].v; if(top[v])continue; dfs2(v,v); } } namespace BIT{ long long c[2][maxn]; inline void add(int k,int x){ for(int p=k;k<=N;k+=lowbit(k)) c[0][k]+=x,c[1][k]+=1ll*p*x; } inline long long ask(int k){ long long sum=0; for(int x=k;k;k^=lowbit(k)) sum+=(x+1)*c[0][k]-c[1][k]; return sum; } inline void add(int l,int r,int v){ add(l,v),add(r+1,-v); } inline long long ask(int l,int r){ return ask(r)-ask(l-1); } } inline void change(int u,int v,int val){ int fu=top[u],fv=top[v]; while(fu^fv){ if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); BIT::add(low[ct[fu]],low[ct[u]],val); u=fa[fu],fu=top[u]; } if(dep[u]>dep[v])swap(u,v); BIT::add(low[ct[u]],low[ct[v]],val); } inline long long ask1(int u,int v){ long long sum=0; int fu=top[u],fv=top[v]; while(fu^fv){ if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); if(down[fu]<=low[u]) sum+=BIT::ask(down[fu],low[u]); u=fa[fu],fu=top[u]; } if(dep[u]>dep[v])swap(u,v); if(down[u]<=low[v]) sum+=BIT::ask(down[u],low[v]); return sum; } inline long long ask2(int u){ return L[u]?BIT::ask(L[u],R[u]):0; } bool in[maxn]; void dfs3(int u){ if(in[u])low[u]=++N; if(!son[u]){ L[u]=R[u]=low[u]?low[u]:0; return; } dfs3(son[u]); L[u]=low[u]?low[u]:L[son[u]]; for(int i=head[u];i;i=e[i].nxt){ int v=e[i].v; if((v^fa[u])&&(v^son[u])) dfs3(v); } R[u]=N; } inline void init(){ dfs1(1); dfs2(1,1); for(int t=1;t<=n;t++){ if(!d[t].size())continue; ct[d[t].back()]=d[t].back(); in[d[t].back()]=1; for(int i=d[t].size()-2;~i;i--){ int u=d[t][i]; ct[u]=ct[d[t][i+1]]; while(size[ct[u]]<=size[u]/2) ct[u]=fa[ct[u]]; in[ct[u]]=1; } } dfs3(1); for(int t=1;t<=n;t++){ if(!d[t].size())continue; down[d[t].back()]=low[d[t].back()]; for(int i=d[t].size()-2;~i;i--){ int u=d[t][i]; down[u]=low[u]?low[u]:down[d[t][i+1]]; } for(int i=1;i<(int)d[t].size();i++){ int u=d[t][i]; low[u]=low[u]?low[u]:low[d[t][i-1]]; } } } } inline void work(){ int opt=read<int>(); int u=read<int>(); if(opt==2){ printf("%lld\n",T_C::ask2(u)); return; } int v=read<int>(); if(opt==1)T_C::change(u,v,read<int>()); else printf("%lld\n",T_C::ask1(u,v)); } int main(){ n=read<int>(); for(int i=1;i<n;i++){ int u=read<int>(); int v=read<int>(); a_e(u,v),a_e(v,u); } T_C::init(); int t=read<int>(); while(t--)work(); return 0; } ``` Loading... ## 问题引入 给定一棵 $n$ 个点的树,求以每个点为根的子树的重心。 数据范围:$n \leq 2 \times 10^5$ ## 朴素方法 $O(n^2)$ 对每个点求出重心,时间无法承受。 ## 方法一 考虑到重心的性质:一个子树的重心一定在其根节点所在重链上。发现重心的定义等价于重心的最大子树不超过整棵子树的一半,因此直接在重链上向下倍增即可。 时间复杂度:$O(n \log n)$ 代码: ```cpp int get(int x, int rt) { return std::max(siz[rt] - siz[x], siz[son[x]]); } void dfs1(int u) { if (siz[son[u]] <= siz[u] / 2) tag[ctr[u] = u] = 1; for (int i = head[u], v; i; i = edge[i].nxt) { v = edge[i].to; if (v == fa[u]) continue; dfs1(v); int c = ctr[v]; if (ctr[u] || siz[v] <= siz[u] / 2) continue; while (fa[c] && get(c, u) > siz[u] / 2) c = fa[c]; while (fa[c] && get(fa[c], u) <= siz[u] / 2) c = fa[c]; tag[ctr[u] = c] = 1; } } ``` ## 方法二 还想再优秀一点?试图求得 $O(n)$ 的做法。 有一个假的结论,可以让你爆零:重心只有可能是儿子的重心、儿子重心的父亲和它自己。在这些点组成的可能集合中找子树大小最大的。 还有一个假的结论:重链上连续的一段节点的重心也是该重链上连续的一段节点。 这两个结论为什么假掉了,我们可以构造一棵树,使得存在点不是任何子树的重心。如图:  例如在一个应用中,每次修改的点都是重心。 其中标黄的边为重边,未标黄的为轻边。如果我们更新重链上连续的一段:1,2,4。那么对应的需要修改的重心为 1,4。并不是连续的一段。 所以上述结论是假的。 稍微将这个结论换一下就真了:即对于任意节点 $u$ ,以它为重心的节点一定和 $u$ 在同一条重链上并且为连续的一段。 有了这个结论,结合重链的性质:$\sum$ 重链长度 是 $O(n)$ 级别的,我们可以找到 $O(n)$ 做法。 以 20210923 CDQZ NOIp模拟赛中秋特别版 T2为例,代码如下:(by CJ_wyz) ```cpp #include<cstdio> #include<cctype> #include<set> #include<ctime> #include<cmath> #include<queue> #include<vector> #include<bitset> #include<random> #include<cstring> #include<cstdlib> #include<algorithm> #define mp std::make_pair #define swap std::swap #define lowbit(k) (k&(-k)) #define mod 31607 template<class T> inline T read(){ T r=0,f=0; char c; while(!isdigit(c=getchar()))f|=(c=='-'); while(isdigit(c))r=(r<<1)+(r<<3)+(c^48),c=getchar(); return f?-r:r; } template<class T> inline T min(T a,T b){ return a<b?a:b; } template<class T> inline T max(T a,T b){ return a>b?a:b; } #define ll long long inline ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; } inline ll lcm(ll a,ll b){ return a/gcd(a,b)*b; } inline ll qpow(ll a,int b){ ll ans=1; for(;b;b>>=1){ if(b&1)(ans*=a)%=mod; (a*=a)%=mod; } return ans; } #undef ll struct Z{ #define add(x) (x>=mod?x-mod:x) #define sub(x) (x<0?x+mod:x) int x; inline int val() const{ return x; } inline int inv() const{ return qpow(x,mod-2); } Z(int x=0):x(x) {} Z operator -() const{ return Z(add(mod-x)); } Z &operator +=(const Z &z){ x=add(x+z.x); return *this; } Z &operator -=(const Z &z){ x=sub(x-z.x); return *this; } Z &operator *=(const Z &z){ x=1ll*x*z.x%mod; return *this; } Z &operator /=(const Z &z){ x=1ll*x*z.inv()%mod; return *this; } Z operator +(const Z &z) const{ return Z(add(x+z.x)); } Z operator -(const Z &z) const{ return Z(sub(x-z.x)); } Z operator *(const Z &z) const{ return Z(1ll*x*z.x%mod); } Z operator /(const Z &z) const{ return Z(1ll*x*z.inv()%mod); } #undef add #undef sub }; #define maxn 202202 struct E{ int v,nxt; E() {} E(int v,int nxt):v(v),nxt(nxt) {} }e[maxn<<1]; int n,s_e,head[maxn],ct[maxn]; inline void a_e(int u,int v){ e[++s_e]=E(v,head[u]); head[u]=s_e; } int L[maxn],R[maxn]; std::vector<int> d[maxn]; namespace T_C{ int s_dfn,fa[maxn],dfn[maxn],dep[maxn],size[maxn]; int N,low[maxn],down[maxn],top[maxn],son[maxn]; void dfs1(int u){ size[u]=1; dep[u]=dep[fa[u]]+1; for(int i=head[u];i;i=e[i].nxt){ int v=e[i].v; if(size[v])continue; fa[v]=u,dfs1(v); size[u]+=size[v]; if(size[son[u]]<size[v])son[u]=v; } } void dfs2(int u,int t){ top[u]=t; dfn[u]=++s_dfn; d[t].push_back(u); if(!son[u]){ R[u]=s_dfn; return; } dfs2(son[u],t); for(int i=head[u];i;i=e[i].nxt){ int v=e[i].v; if(top[v])continue; dfs2(v,v); } } namespace BIT{ long long c[2][maxn]; inline void add(int k,int x){ for(int p=k;k<=N;k+=lowbit(k)) c[0][k]+=x,c[1][k]+=1ll*p*x; } inline long long ask(int k){ long long sum=0; for(int x=k;k;k^=lowbit(k)) sum+=(x+1)*c[0][k]-c[1][k]; return sum; } inline void add(int l,int r,int v){ add(l,v),add(r+1,-v); } inline long long ask(int l,int r){ return ask(r)-ask(l-1); } } inline void change(int u,int v,int val){ int fu=top[u],fv=top[v]; while(fu^fv){ if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); BIT::add(low[ct[fu]],low[ct[u]],val); u=fa[fu],fu=top[u]; } if(dep[u]>dep[v])swap(u,v); BIT::add(low[ct[u]],low[ct[v]],val); } inline long long ask1(int u,int v){ long long sum=0; int fu=top[u],fv=top[v]; while(fu^fv){ if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); if(down[fu]<=low[u]) sum+=BIT::ask(down[fu],low[u]); u=fa[fu],fu=top[u]; } if(dep[u]>dep[v])swap(u,v); if(down[u]<=low[v]) sum+=BIT::ask(down[u],low[v]); return sum; } inline long long ask2(int u){ return L[u]?BIT::ask(L[u],R[u]):0; } bool in[maxn]; void dfs3(int u){ if(in[u])low[u]=++N; if(!son[u]){ L[u]=R[u]=low[u]?low[u]:0; return; } dfs3(son[u]); L[u]=low[u]?low[u]:L[son[u]]; for(int i=head[u];i;i=e[i].nxt){ int v=e[i].v; if((v^fa[u])&&(v^son[u])) dfs3(v); } R[u]=N; } inline void init(){ dfs1(1); dfs2(1,1); for(int t=1;t<=n;t++){ if(!d[t].size())continue; ct[d[t].back()]=d[t].back(); in[d[t].back()]=1; for(int i=d[t].size()-2;~i;i--){ int u=d[t][i]; ct[u]=ct[d[t][i+1]]; while(size[ct[u]]<=size[u]/2) ct[u]=fa[ct[u]]; in[ct[u]]=1; } } dfs3(1); for(int t=1;t<=n;t++){ if(!d[t].size())continue; down[d[t].back()]=low[d[t].back()]; for(int i=d[t].size()-2;~i;i--){ int u=d[t][i]; down[u]=low[u]?low[u]:down[d[t][i+1]]; } for(int i=1;i<(int)d[t].size();i++){ int u=d[t][i]; low[u]=low[u]?low[u]:low[d[t][i-1]]; } } } } inline void work(){ int opt=read<int>(); int u=read<int>(); if(opt==2){ printf("%lld\n",T_C::ask2(u)); return; } int v=read<int>(); if(opt==1)T_C::change(u,v,read<int>()); else printf("%lld\n",T_C::ask1(u,v)); } int main(){ n=read<int>(); for(int i=1;i<n;i++){ int u=read<int>(); int v=read<int>(); a_e(u,v),a_e(v,u); } T_C::init(); int t=read<int>(); while(t--)work(); return 0; } ``` 最后修改:2021 年 09 月 24 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏
3 条评论
不是说托老师的一定切了吗
不是说我的一定假了吗
那肯定不是我说的